cmass.html

Suppose we have a wire feet long whose density is pounds per foot at the point feet from the left hand end of the wire. What is the total mass of the wire and where is its center of mass , i.e., the point cm about which the total moment of the wire is 0?

Mass Chop the wire into n small pieces each feet long and pick an arbitrary point in each piece. An approximation to the mass of the ith piece of wire is , so an approximation to the total mass is . This approximate mass is a Riemann sum approximating the integral 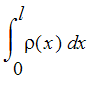, and so the mass of the wire is defined as the value of this integral.

Center of mass : Chopping as above, the approximate moment of the ith piece about the center of mass cm is and so the total approximate moment is . This is seen to be a Riemann sum approximating the integral 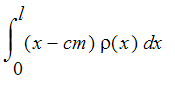. But the center of mass is defined as the point about which the total moment is zero so the integral satisfies the equation 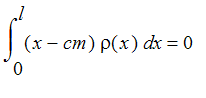. Using properties of integrals, we can solve this equation for cm, to get the ratio of integrals 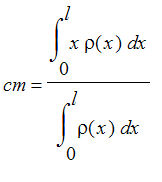. Note the top integral represents the total moment of the wire about its left end (x=0) and the bottom integral is the total mass of the wire.

Exercise: Find the center of mass of a wire 1 foot long whose density at a point x inches from the left end is 10 + x + sin(x) lbs/inch.

Center of mass of a solid of revolution

If for , then let S be the solid of revolution obtained by rotating the region under the graph of f around the x axis. We know how to express the volume of S as an integral: Just integrate from a to b the crossectional area 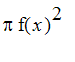of the solid S to get

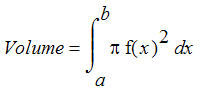
Now how would we find the center of mass of the solid, assuming it's made of a homogeneous material? Well, it's clear that the center of mass will be somewhere along the x-axis between a and b. Let CM be the center of mass. Partition into n subintervals and using planes perpendicular to approximate the solid S with the n disks where the ith one has volume

Now the signed moment of the ith disk about the point CM is and the sum of these moments will be approximately 0, since CM is the center of mass. If we let go to zero this approximate equation becomes an equation for the center of mass:

> CMequation := int((x-CM)*Pi*f(x)^2,x=a..b) =0;

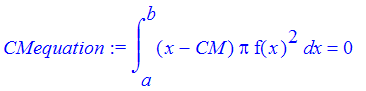
Useing properties of integrals, we can solve this equation for CM.

> sol := solve(CMequation,{CM} ) ;

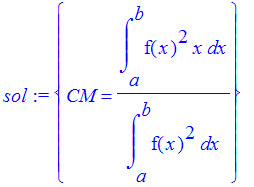
$sol := {CM = int(f(x)^2*x,x = a .. b)/int(f(x)^2,x = a .. b)}$

Notice that the center of mass of the solid of revolution is the same as the center of mass of a wire whose density at is the area of the cross-section.

We can define a word cenmass which takes a function f, an interval [a,b], and locates the center of the solid of revolution.

> cenmass := proc(f,a,b)
int(x*f(x)^2,x=a..b)/int(f(x)^2,x=a..b) end:

For example, the center of the solid obtained by rotating the region R under the graph of for x between 0 and is

> cenmass(cos,0,Pi/2);

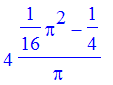
Now we can define a word to draw the solid and locate the center of mass.

>    drawit := proc(f,a,b)
local cm, solid;
### WARNING: the definition of the type `symbol` has changed'; see help page for details
  cm := plots[pointplot3d]([evalf(cenmass(f,a,b)),0,0],color=red,symbol=box,thickness=3):
  solid := plots[tubeplot]([x,0,0],x=a..b,radius=f(x),numpoints=20,style=wireframe);
plots[display]([cm,solid],scaling=constrained); end:

Test this out.

> drawit(cos+2,0,7);

We can animate the motion of the center of mass as the solid changes.

> plots[display]([seq(drawit(2+cos,0,t),t=1..10)],
insequence=true);

Exercise: Find the center of mass of a homogeneous hemispherical solid.

Exercise: A homogeneous solid is in the shape of a parabolic solid of revolution obtained by rotating the graph of y = x^2 , x in [0,a] around the the y axis, for some positive number a. If the center of mass is at y= 10, what's a?