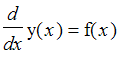 , where f is some known function of x and y is an unknown function of x. These are solved by antidifferentiation. We use
int
. For example, to solve the differential equation y'(x)= x^2*cos(x), we would type
, where f is some known function of x and y is an unknown function of x. These are solved by antidifferentiation. We use
int
. For example, to solve the differential equation y'(x)= x^2*cos(x), we would type
The simplest differential equation is of the form
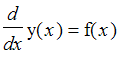 , where f is some known function of x and y is an unknown function of x. These are solved by antidifferentiation. We use
int
. For example, to solve the differential equation y'(x)= x^2*cos(x), we would type
, where f is some known function of x and y is an unknown function of x. These are solved by antidifferentiation. We use
int
. For example, to solve the differential equation y'(x)= x^2*cos(x), we would type
| > | y := int(x^2*cos(x),x) + C; |
![]()
The constant of integration C can be determined once you know a single value of the function. So if y(3) = 10, then we can get C by solving an equation.
| > | Csol := solve(subs(x=3,y=10),{C}); |
![]()
| > | y := subs(Csol,y); |
![]()
| > | plot(y,x=-6..6); |
![[Maple Plot]](images/diffeq5.gif)
| > |
The theorem which tells us about uniqueness of solutions is the following.
Big theorem: If two functions have the same derivative on an interval, they differ by a constant.
A differential equation is an equation which expresses a relation between an unknown function y and one or more of its derivatives. A solution to the differential equation is a function which satisfies the equation.
An Initial Value Problem or IVP is a differential equation together with some initial conditions. A solution to the IVP is a function which satisfies the equation and also the intial conditions.
The order of a differential equation is n where n is the highest order derivative appearing in the equation.
We will concentrateon first order equations of the form y' = f(x,y). Many interesting problems lead to a first order equation of some sort.
The Maple word dsolve takes as input a differential equation and possibly some initial values, and attempts to return a solution to the equation.
To illustrate how dsolve works, use it to solve the above differential equation.
| > | restart; |
Set up the differential equation.
| > | diffeq := diff(y(x),x)=x^2*cos(x); |
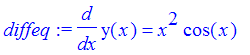
use dsolve on it.
| > | dsolve(diffeq,y(x)); |
![]()
Note the constant of integration. If we include the initial conditions, dsolve will determine this constant.
| > | inits := y(3) = 10; |
![]()
| > | sol := dsolve({diffeq,inits},y(x)); |
![]()
Now to plot sol we can just plot the right hand side (rhs) of the solution:
| > | plot(rhs(sol),x=-6..6); |
![[Maple Plot]](images/diffeq10.gif)
or we could turn sol into a function with unapply.
| > | f := unapply(rhs(sol),x); |
![]()
There is a useful package of words to use called DEtools .
| > | with(DEtools); |
![]()
![]()
The word dfieldplot is one which you can use to examine qualitatively the solution curves to a differential equation y' = f(x,y). For example for the diffeq above,
| > | dfieldplot(diffeq,[y(x)],x=-6..6,y=-10..40,title=`The direction field of y' = x^2*cos(x).`); |
![[Maple Plot]](images/diffeq14.gif)
By looking at the direction field plot, you can visually sketch in the solution curves to the differential equation. Another term for solution curve is integral curve. An isocline is a curve that connects points where the slope is constant. For example, the isoclines of the differential equation above are the vertical lines. When you are forced to construct a direction field plot by hand, it is often easier to first sketch in a few isoclines before drawing in the slope vectors.
Problems leading to first order equations
A Salt tank problem
Setting: A tank initially contains 50 gallons of fresh water. Brine containing 1/4 lb salt/gal comes into the tank at 3 gals /minute and the solution is kept homogeneous by vigorous stirring. The mixture drains out of the tank at 3 gals /minute, so that there is always 50 gallons of solution in the tank.
Even before we think of a differential equation, we can make a rough sketch of the amount of salt in the tank over time. Let A(t) be the amount of salt in the tank at time t. Then A(0) = 0, and as t increases towards infinity A(t) will increase towards 50*1/4 lbs.
Now we don't know A(t) explicitly, but we can say what the rate of change of A(t) with respect to t is, and this will be the differential equation we need to solve. In words, the rate of change of A(t) is the rate at which the salt is coming in minus the rate at which it is going out. The in rate is constant, at 3*1/4 lbs per minute. The out rate is increasing: At any particular time t, the concentration of the salt in the tank is A(t)/50 lbs per gallon, so the salt is going out at 3* A(t)/50 lbs per minute. This give the differential equation which governs the amount of salt in the tank.
| > | diffeq := diff(A(t),t) = 3/4 - 3*A(t)/50; |
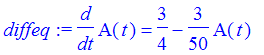
The initial value of A(t) is A(0)=0, so we should get a unique solution from dsolve.
| > | ### WARNING: `dsolve` has been extensively rewritten, many new result forms can occur and options are slightly different, see help page for details sol := dsolve({diffeq,A(0)=0},A(t)); |
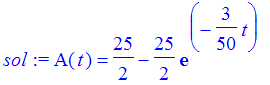
| > | plot(rhs(sol),t=0..100); |
![[Maple Plot]](images/diffeq17.gif)
We can make a function from sol and use it to answer any question about the setting.
| > | A := unapply(rhs(sol),t); |
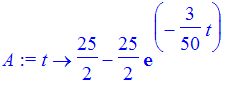
For example, what is the amount of salt in the tank after 1 minute? Answer:
| > | A(1.),`lbs`; |
![]()
How long does it take the amount of salt in the tank to get to 10 lbs? Answer:
| > | solve(A(t)=10,t); |
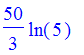
| > | evalf(%),`minutes`; |
![]()
We can solve the differential equation coming out of the salt tank problem 'by hand', because it is separable equation . That is, it is of the form y' = f(x)*g(y). Separable equations always reduce to finding two antiderivatives. Just rewrite the equation in the form y'/g(y) = f(x) and antidifferentiate both sides. If you are successful, you will have an equation in x and y(x) only. This equation implicitly defines the solutions to your separable equation. Sometimes you can solve the equation for y(x). Then you have found an explicit solution to the separable equation. In our case,
| > | restart; |
| > | diffeq := diff(A(t),t) = 3/4 - 3*A(t)/50; |
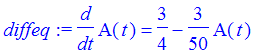
We rewrite this in the A' = 3/4-3/50*A=f(t)g(A), where f(t) = 1 and
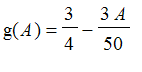 . Now an antiderivative of f(t) = 1 is t + C, and an antiderivative of A'/g(A), we can get by substitution. The equation we get after integrating both sides is
. Now an antiderivative of f(t) = 1 is t + C, and an antiderivative of A'/g(A), we can get by substitution. The equation we get after integrating both sides is
| > | eq := int(1/(3/4-3/50*A),A)= int(1,t)+C; |
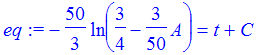
To determine the constant of integration here, use the given initial value of A=0 when t=0.
| > | Csol := solve(subs({A=0,t=0},eq),{C}); |
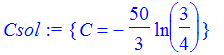
| > | assign(Csol); |
Now solve for A and make it into a function.
| > | A := unapply(solve(eq,A),t); |
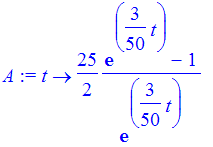
Look ma, no dsolve!
Exercise: Suppose the salt tank develops a leak at time t=0, from which an additional 1/2 gallon of solution per minute leaves the tank. How do you think this will affect the function A(t)? Make a sketch to accompany your discussion. Write down the new differential equation which governs the setting. Is it separable? Solve it with dsolve and plot over the appropriate time interval. What is the maximum amount of salt in the tank and when is it there?
| > |
| > |
Radioactive decay: Carbon 14 dating
Problem: A piece of charcoal found at Stone Henge was determined to contain Carbon 14 in a concentration which produced 8.2 disintegrations per minute per gram. Charcoal from a living tree is known to produce 13.5 disintegrations per minute per gram. The half life of Carbon 14 is known to be 5568 years. Assuming that the tree was burned during the construction of Stone Henge, estimate the age of Stone Henge.
A Solution:
The law of radioactive decay was discovered by experiment. It is simply that radioactive materials decay (or turn into non-radioactive materials) at a rate which is proportional to the amount of radioactive material present. We set up the differential equation so that the decay constant, k, is positive.
| > | diffeq := diff(decay(t),t) = -k*decay(t); |
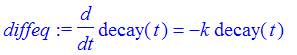
A gram of the charcoal back when Stone was being built (t=0) had enough carbon 14 to provide 13.5 disintegrations per minute, and now at t=T has enough to provide only 8.2 disintegrations per minute. We will use the number of disintegrations per minute as our measure of the amount of carbon 14 in the gram of charcoal. With that understood, the initial condition then is
| > | conds := decay(0)=13.5; |
![]()
We could solve this by hand, but for the moment use dsolve.
| > | ### WARNING: `dsolve` has been extensively rewritten, many new result forms can occur and options are slightly different, see help page for details soln := dsolve({diffeq,conds},decay(t)); |
![]()
Make a function of the right hand side.
| > | decay := unapply(rhs(soln),t); |
![]()
Now determine the decay constant k. This we can do by using the half life information. Every 5568 years, the amount of carbon 14 in a gram of the charcoal is cut in half (and so the number of disintegrations per minute is cut in half).
| > | k := solve(decay(5568)=1/2*decay(0),k); |
![]()
Now we can use the measurement of 8.2 disintegrations per minute per gram to estimate the age of Stone Henge.
| > | age_of_Stone_Henge := solve(decay(t)=8.2,t); |
![]()
So, Stone Henge was built right about the time the world was made (according to Bishop Usher).
Exercise: Solve the differential equation in the problem above by hand, using the fact that it is separable.
Logistic growth occurs when the rate of change of a population is proportional to the product of the population present and the amount of room left. This is a differential equation. k is the constant of proportionality and C is the least upper bound on the population.
| > | deq := diff(p(t),t)=k*p(t)*(C-p(t)); |
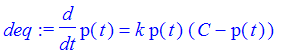
This equation is separable and can be solved symbolically.
| > | ### WARNING: `dsolve` has been extensively rewritten, many new result forms can occur and options are slightly different, see help page for details sol := dsolve(deq,p(t)); |
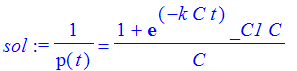
Seems like a strange way to write the solution. Lets turn it right side up.
Also, we can replace the constant C1*C with C1 no problem.
| > | p := t-> C/(1+C1*exp(-k*C*t)); |
| > |
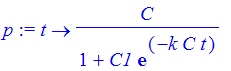
By looking at the population function, we can see that as t goes to infinity p(t) goes to C. If we are going to model a population with the logistic equation, we need to know the population at three times, in order to get three equations to determine the three parameters k, C, and C1 in the population function.
Suppose you measured the population at three times and got p(0) = 10000, p(10) = 20000, and p(20) = 30000. Looks linear doesn't it? What logistic curve fits this data?
Set up the equations.
| > | eq1 := p(0) = 10000; |
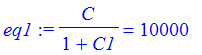
| > | eq2 := p(10) = 20000; |
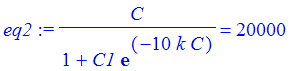
| > | eq3 := p(20) = 30000; |
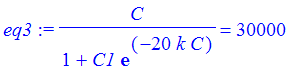
Then solve for the parameters.
| > | sln :=solve({eq1,eq2,eq3},{C,C1,k}); |
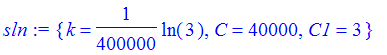
Make a function out of the solution.
| > | f := unapply(subs(sln,p(t)),t); |
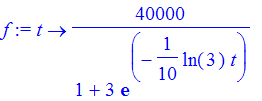
Draw a picture of the population curve.
| > | plot([40000,f],0..70,color=black); |
![[Maple Plot]](images/diffeq41.gif)
Where is the inflection point? In general, it will be at
| > | solve(diff(p(t),t,t),t); |
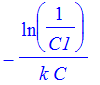
For our particular data, it will be at
| > | solve(diff(f(t),t,t),t); |
![]()
Question: What happens to the population curve as the population at t = 20 changes?
Introduce a parameter p20 to stand for the population at t=20 and resolve.
| > | eq3 := p(20) = p20; |
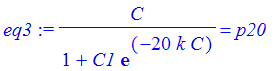
| > | sln := solve({eq1,eq2,eq3},{C,C1,k}); |
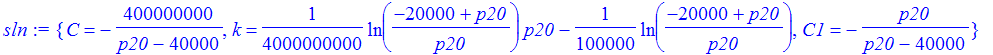
By inspection, we can see that p20 must be greater than 20000 and less than 40000.
Make a function again, this time with two variables, t and p20
| > | f := unapply(subs(sln,p(t)),t,p20); |
![]()

Now we can animate the change in the population curve as the population at t=20 runs through its possible values. Unfortunately, you can't see the animation if you are looking at a piece of paper.
| > | plots[animate](f(t,p20),t=0..150,p20=21000..39000); |