hand2.html

An introduction to the Maple language

This section contains an introduction to some of the Maple vocabulary used for solving problems. It is not meant to cover everything, just some of the basics. Read it through quickly, to get an overview of the language. Then you can come back and read with more understanding later.

Arithmetic

First, there is arithmetic: addition, subtraction, multiplication, division and exponentiation. These can be combined, just as on a calculator. The order of precedence is the the usual one: exponentiation first, then multiplication and division, then addition and subtraction. So entering

> 2-3+4/5*6^7;

is the same as entering

> (2-3)+(4/5)*(6^7);

You will notice that Maple works with fractions whenever possible, changing to decimal numbers only on demand. So typing and entering (pressing the enter key)

> 1/3 + 1/2;

will get a return of 5/6. If you put a decimal point in one of the numbers, that forces Maple to return a decimal answer.

> 1/3. + 1/2;

Another way to get decimals is to use the maple word evalf to convert a result to decimal form.

> evalf(1/2+1/3);

Maple does arithmetic with complex numbers too. I is a Maple constant standing for . So entering

> (3+2*I)*(2-I);

>

will produce an output of 8+I .

The name for pi, the area of the circle of radius 1, in Maplese is Pi. So to calculate the area of a circle of radius 3, you would enter

> Pi*3^2;

>

Expressions, Names, Statements, and Assignments

Quantities to be computed like 1/2+1/3 are called expressions.

A name is a string of characters which can be used to store the result of a computation.

A statement in Maple is a string of names and expressions terminated with a semicolon, or a colon if you don't want to see the output, which when entered will produce some action.

The assignment statement is one of the most common statements. It is of the form

name := expression; For example, the assignment

> area := Pi*3^2;

stores 9*Pi in a location marked by the name area.

A more useful assignment for the area of a circle is

> area := Pi*r^2;

In this case, the expression Pi*r^2 is stored in area and with this assignment, the area of a circle of any given radius can be computed using the Maple word subs. So to calculate the area when r is 3, we enter

> subs(r=3,area);

Here, it is convenient to think of the assignment as defining area as a function

of the radius r.

Functions

A function is a rule f (possibly very complicated) for assigning to each argument x in a given set, a unique value f(x) in a set. In calculus the arguments and values of a function are always real numbers, but the notion of function is much more flexible than that.

Functions can be defined in several useful ways in Maple.

As an expression: The assignment

> area := Pi*r^2;

defines the area of a circle as a function of it's radius. The area function defined as an expression is evaluated with subs. Since this function assigns real numbers to real numbers, its values can be plotted on a graph with the Maple word plot. So the statement

> plot(area,r=0..4);

will produce in a separate plot window, the graph of the area function over the interval from r=0 to r=4 .

With the arrow operator the assignment: If you have a simple function, you can often use the arrow operator . For example,

> area := r -> Pi*r^2;

defines the area function also. Now to find the area of a circle of radius 3, we simply enter the statement

> area(3);

To plot this function over the domain r=0..4 , type

> plot(area,0..4);

Note that the variable r is omitted here.

Use unapply . The ugly little word unapply transforms expressions of one or more variables into fuctions defined by an arrow operator. For example, if we had a polynomial defined by the assignment

> pol := x^2 + 4*x -1;

then the assignment

> pol := unapply(pol,x);

turns pol into a function defined by an arrow operator.

As a procedure: The Maple word proc can be used to define functions. For example,

> area := proc(r) Pi*r^2 end;

defines the area function too. It is evaluated and plotted as in the arrow operator definition. One advantage of this way of defining a function is that the domain can be specified. For example, the domain of the area function for a circle is all positive real numbers. This can be inserted into the procedure, with the Maple word ERROR .

The message must be enclosed in backquotes '`', which is on the key with the tilde .

> area := proc(r)

> if r <= 0 then ERROR(`radius must be positive`) else

> Pi*r^2 fi end;

> area(3);

> area(-3);

Error, (in area) radius must be positive

Note the if..then..fi control statement here.

You can learn more about the word if by typing ?if in an input cell and entering it.

Functions of two variables can be defined and plotted just as easily in Maple as functions of one variable. For example, the volume V of a cylinder of height h and radius r is defined by

> V := (r,h) -> Pi*r^2*h;

To see what the graph of V looks like, use plot3d .

> plot3d(V,0..4,0..4,axes=boxed);

Which way of defining a function is the preferred way? That really depends on the situation. The expression method works well for functions which have only one rule of evaluation, but eventually you cannot avoid using an -> or proc definition. You will find yourself using arrow or proc definitions more and more as time goes by.

Piecewise defined functions:

Many functions can only be described by stating various rules for various parts of the domain. The Maple word piecewise will help with defining such functions.

Here is an example to show usage.

> f(x) :=piecewise(x <= -1,x^3+8, x <= 2,7+ 2*x, x <= 4, 11 - cos(x),3*x);

> f(2);

As it stands, f is not really a function. We need to use unapply to make it into a funtion.

> g :=unapply(f(x),x);

> g(2);

When plotting piecewise defined functions, sometimes style = point is better.

> plot(g, -3..6,style= point);

Built in Maple functions and Operations with Functions

All of the standard scientific functions are built into Maple. For example, sqrt is the square root function, abs is the absolute value function, the trig and inverse trig functions are sin , arcsin , cos , etc., the natural logarithm and exponential functions are ln and exp . For a complete list of built in functions, type

> ?inifcns;

New functions can be obtained from old functions by use of the arithmetic operations of addition, subtraction, multiplication, and division together with the operation of composition, which is denoted by @ . Thus the function defined by the assignment

> y := sin(cos(x^2+3));

and evaluated at x=3 by

> subs(x=3.,y);

could also be defined by the assignment

> y := sin@cos@(x->x^2+3);

and evaluated at x=3 by

> y(3.);

Using Maple as a fancy graphing calculator.

It is convenient to think of Maple as a fancy graphing calculator for many purposes. For example, suppose you want to find the real solutions of the equation 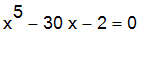in the interval . Then we can just plot the right hand side of the equation and look for where the graph crosses the x-axis.

> f := x -> 10*x^5 - 30*x +10 ;

> plot(f,-3..3);

By inspection, the graph crosses near 0. We can look closer.

> plot(f,-1.5..1.5);

>

We see that the graph crosses 3 times, the largest solution being between 1 and 1.5. If we wanted the largest solution more accurately, we could use fsolve. Note the syntax. There are three arguments, the equation to solve, the variable to solve for, and the interval in which to search for a solution.

> fsolve(f(x)=0,x,1..1.5);

Data types, Expression Sequences, Lists, Sets, Arrays, Tables:

Maple expressions are classified into various data types . For example, arithmetic expressions are classified by whether they are sums type '+' , products type '*' , etc.

The Maple word whattype will tell what type a particular expression is.

> whattype(1/2);

$fraction$

> whattype(a + b);

> whattype(x^2 + x = 2*x - 1);

> whattype(a,b,3);

Expression Sequence.

An exprseq , expression sequence, is any sequence of expressions separated by commas. For example,

> viola := 1,2, w*r+m, a=b+c, 1/2, (x+y)/z,`hello`;

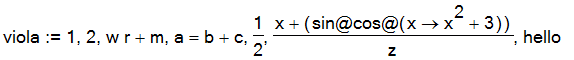
is an assignment to viola of an expression sequence of 7 expressions. To refer to the sixth expression in this sequence, use the expression viola[6];

> viola[6];

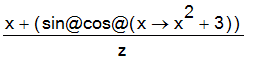
List.

A list is an expression sequence enclosed by square brackets. So

> explist:= [viola];

makes a list whose terms are those in viola . As with expression sequences, we can refer to particular terms of a list by appending to its name the number of the term enclosed in square brackets. Thus to get the fifth term of explist , type the expression

> explist[3];

You can also reference the fifth term in this list by by using the Maple word op .

> op(3,explist);

In general, op(n,explist); returns the nth term in the list explist .

To count how many terms are in a list, use the word nops . So for example,

> nops(explist);

tells us that there are 7 terms in the list explist . nops comes in handy when you

don't want to (or aren't able to) count the terms in a list by hand.

You can't directly use the word nops to count the number of terms in an expression sequence. But you can put square brackets around the expression sequence and count the terms in the resulting list. This device is used again and again.

> nops(3,4,a);

Error, wrong number (or type) of parameters in function nops

> nops([3,4,a]);

A point in the plane is a list of two numbers. Points can be added and subtracted and multiplied by a number.

> p := [1,2]; q := [-3,1];

> w := 3*p + 2*q - p;

One important use of lists is to make lists of points to plot. For example, to draw a picture of the square with vertices (1,1), (3,1), (3,3), (1,3), make a list and then plot it.

> ab := [[1,1],[3,1],[3,3],[1,3],[1,1]];

> plot(ab);

Notice in the graph that the origin is not included in the field of view. We can specify that by restricting the x and y coordinates.

> plot(ab,x=0..4,y=0..4);

Error, (in plot) invalid arguments

Another use of lists is with parametric plots . If you have a curve in the

plane described parametrically with , , as the parameter t runs from a to b, then you can draw it by making up a 3 term list to give to plot. Say you wanted to draw the upper half of the circle of radius 4 centered at (1,5). Then the list consists of the expressions for the x and y coordinates followed by an equation giving the range of the parameter.

> plot([1+4*cos(t),5+4*sin(t),t=0..Pi],
scaling=constrained);

If you had to draw several pieces of circles, you might define a function to simplify things. You can call the function whatever you want, say circ.

> circ := (h,k,r,f,l) -> [h+r*cos(t),k+r*sin(t),t=f..l];

So if we wanted circles of radius 1/2 centered at the corners of the square ab we can construct the sequence of lists

> circs := seq(circ(op(ab[i]), 1/2,0,2*Pi),i=1..4);

In order to plot these circles, you need to enclose them in curly brackets to make a set of the sequence before you give them to plot . See below for a discussion of sets.

> plot({circs,ab},scaling=constrained);

Sometime you might want to split a list of points to plot into a list of x-coordinates and another list of ycoordinates. The Maple word seq is very handy for this and many other operations. So to split off from ab the odd and even terms--

> xdat := [ seq(ab[i][1],i=1..nops(ab) )];

> ydat := [seq(ab[i][2],i=1..nops(ab) )];

What about the converse problem? Building up a list of points to plot from two lists can also be done. The first thing you might think of doesn't work, however.

> seq([xdat[i],ydat[i]],i=1..nops(xdat));

Seq doesn't work well with a pure expression sequence as input. However, with some coaxing we can get it to do what we want.

> newab :=[seq([xdat[i],ydat[i]],i=1..nops(xdat))];

What did we do to change the input to seq ? We enclosed it in square brackets. If you feed such a list of points to plot, it knows what to do. If you wanted to strip out the inside brackets, that can be done too, but in release 4 of Maple, plot would treat it as a sequence of constant functions.

> newab := [seq(op([xdat[i],ydat[i]]),i=1..nops(xdat))];

> plot(newab,color=black);

>

Sets

A set is an expression sequence enclosed by curly brackets. This is much different from a list. For one thing, the order in which you specify the members of a set may not be the order in which they are stored. Also each member of the set is only stored once, no matter how many times you list it.

> Aset := {y+x+1,1,2,1,4,`bill`,x+y+1,`bill`};

$Aset := {1, 2, 4, bill, `@`(sin,cos,proc (x) options operator, arrow; x^2+3 end proc)+x+1}$

The set operations of union, intersection , and minus are at your beck and call.

> Anotherset := Aset union {4,3,a,7} ;

$Anotherset := {1, 2, 3, 4, 7, a, bill, `@`(sin,cos,proc (x) options operator, arrow; x^2+3 end proc)+x+1}$

> Anotherset minus Aset, Anotherset intersect Aset;

${3, 7, a}, {1, 2, 4, bill, `@`(sin,cos,proc (x) options operator, arrow; x^2+3 end proc)+x+1}$

Sets are important when plotting more than one function at at time, to plot the quadratic function 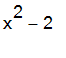and the linear function on the same axes,

> plot({x^2-2,2*x+5},x=-5..5);

>

plots the parabola 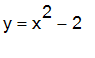and the line over the domain on the same graph. If you have a very complicated drawing to make, you can use plots[display] from the plots package. Just give names to the plots you want to display and then display the list of plots you have named.

> pl1 := plot({x^2-2,2*x+5},x=-5..5):

> pl2 := plot([[2,1],[3,20],[0,0],[2,1]]):

> plots[display]([pl1,pl2]);

>

Tables and Arrays

A table is a special kind of data structure which is very flexible. The packages of special vocabularies are really tables whose indices of the package are the names of the procedures and whose entries are the bodies of the procedures. We do not make much use of tables in this handbook, except for arrays.

An array is a special kind of table whose indices are numerical. Somet useful arrays are matrices (2 dimensional arrays) and vectors (1 dimensional arrays).

Matrix operations are made using Maple word evalm together with the symbol for matrix multiplication &* .

> a := array(1..2,1..2);

>

creates a 2 by 2 matrix, whose entries are accessed as a[1,1] etc.

So to rotate the square through an angle of 31 degrees counter clockwise about the origin and display it, we could proceed as follows.

> rot := array([[cos,-sin],[sin,cos]]);

> ang := evalf(Pi/180*31);

> ab := [[1,1],[3,1],[3,3],[1,3],[1,1]];

> rotab := [seq(convert( evalm(rot(ang)&*ab[i]),list) ,i=1..nops(ab) )];

> plot({ [[0,0]],ab,rotab} );

Maple control statements

There are two especially important control statements . One is the repetition loop , and the other is the conditional execution statement. The repetition loop is

for .. from .. by .. to .. while .. do .. od;

This statement can be used interactively or in a procedure to perform repetitive tasks or to do an iterative algorithm.

Example: Add up the first 100 numbers.

> s := 0: for i from 1 to 100 do s := s+i od:

> s;

Example: Compute the cubes of the first five positive integers and store them in a list. Then do it again, storing them in an array.

Solution with lists:

> locube := NULL: # start with the empty exprseq
for i from 1 to 5 do
locube := locube ,i^3 od:
locube := [locube]; # make locube a list.;

>

Note the way the list is built up from an empty exprseq NULL . Each time through the loop, one more term is added onto the end of the sequence. At the end, square brackets are put around the sequence, making it a list. With arrays, one can be more direct.

Solution with arrays:

> aocube := array(1..5): # initialize the array.

> for i from 1 to 5 do aocube[i]:= i^3 od;

> op(aocube); # to see the array

>

Now the array aocube has the numbers stored in it. To refer to the third element of aocube , we would enter aocube[3] just as if it were a list, rather than an array. Why have arrays at all? Well, for one thing, the terms in an array can be more easily modified. For example, to change the third term in aocube to 0 just enter ; . To change the third term in locube to 0, you have to make an entirely new list whose terms are all the same as locube except for the third one.

> aocube[3]:=0;

> print(aocube);

> locube := [locube[1],locube[2],0,locube[4],locube[5]];

>

Conditional execution

if .. then .. elif .. else .. fi;

There are lots of times when you need to consider cases, and they can all be handled with the if .. then .. elif .. else .. fi; statement. For example, many functions are defined piecewise. The absolute value function abs is such a function.

Problem: Define your own version of the absolute value function.

A solution:

> myabs := proc(x) if x > 0 then x else -x fi end;

> myabs(-23);

> plot(myabs,-2..2,scaling=constrained,title=`my absolute value`); # to see what it looks like.

A Brief Vocabulary of Maple Words

Here are some Maple words useful in calculus problem solving, together with examples of their usage. For more information on these words and others, look at the helpsheets and use the help browser.

> y := (x+3)/tan(x^2-1); # use 'colon-equal' to make assignments.

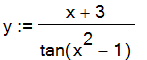
> collect(x*2 + 4*x,x); # collects like powers of x.

> diff(cos(x),x); # calculates the derivative

> D(cos); # the differential operator

> y := denom((a+b)/(e+f)); # assigns e+f to y.

> y := 'y'; # makes y a variable again.

> evalc((2+3*I)^3); # performs complex arithmetic

> evalf(1/2^9); #evaluates 1/2^9 to a decimal number

> expand((x+b)^7); # expands the product

> p := x^2+5*x+6; # assigns the quadratic to p.

> factor(p); # factors the polynomial

> fsolve(x^5-3*x=1,x,0..2); # solve eqn for x in 0..2

> int(x*exp(x),x); # returns an antiderivative.

> Int(x*exp(x),x=0..1); # A passive integral.

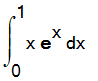
> map(x->x^2,[1,3,2,5]); # returns a list of squares.

> nops([3,4,x,1]); # returns the number of terms in the list.

> numer((a+b)/c); # gives numerator, here a+b

> op([3,4,1,x]); # strips the brackets off the list

> plot(x^2+x, x=-3..3); # plots x^2+x as x goes from -3 to 3.

> plot3d(x^2+y,x=-2..2,y=0..2); # plots a surface

> f := x -> x^2; # defines the squaring function.

> f(3); # then returns 9.

> quo((x^4-4),(x^2-2),x); # divides polynomials

> iquo(23,2) ; # divides the integers

> rem((x^4-4*x+3),(x^2-2),x); # gives the remainder

> irem(23,2) ; # gives the integer remainder

> restart; # very handy. This word resets all assignments.

> eq1 := x^2 + 3*x -1 = a; # assigns the equation

> rhs(eq1); # yields the righthand side of eq1. There is also an lhs.

> simplify(a/x+b/y); # sometimes simplifies expr.

> solve(a*x+4*y=0,x); # solve the equation for x.

> subs(x=5,x^2+x); # substitute 5 for x where it occurs in x^2+x.

> i := 'i'; # makes i a variable again

> sum((i^2,i=2..9)); # add up the 2nd thru 9th squares

>

Trouble Shooting Notes

Learning to use Maple can be an extremely frustrating experience, if you let it. There are some types of errors which occur from the beginning that can be spotted and corrected easily by a person fluent in Maple, so if you have access to such a person, use him or her.

Here are a few suggestions that may be of use when you're stuck with a worksheet that's not working like it should.

Use help: There is a help sheet with examples for every Maple word. A quick read thru will often clear up syntax problems. One very common early mistake is to leave out the parentheses around the inputs of a word. For example, typing

> plot x^2;

Error, missing operator or `;`

will get you a syntax error, because you left out the parentheses.

>

The maple prompt is `>` . You can begin entering input after it. Make sure you are typing into an input cell, if you are expecting output.

End maple statements with a semicolon `;` . Maple does nothing until it finds a semicolon. If you are getting no output when you should be, try feeding in a semicolon. This often works.

When in doubt, put in parentheses. For example, (x+3)/(x-3) is very different from x+3 / x-3 .

Make sure your variables are variable. You may have assigned a value, say 3, to x in a previous problem. To make x a variable again, type x := 'x': . Use the forward quote ' key, just below the double quote " here. If you forget this, strange things can happen. One way to handle this is to keep an input cell of variables used.

Use restart; By typing restart; in an input cell and pressing enter, you clear all assignments, and start with a clean slate. This fixes a lot of problems fast, but you will need to re-execute input cells.

Are you using the correct quote symbol? In Maple, the forward quote ' is used to suppress evaluation. The back quote ` is used to enclose ascii strings. The double quote " is used to reference the last computation.

Do not forget to end loops with od, `if` statements with fi, and procedures with end. If you start a loop with do , Maple does not begin processing until it finds the end of the loop, which is signaled by the word od; The same applies to the if .. then ... fi; and proc ... end; contructions. If you are getting no output when you should be, try feeding an od; , fi; , or end; This often works.

Unwanted output?: Is there output you need but don't want to see? Use a colon `:` instead of a semicolon to end the Maple statement which generates the output.

Use printlevel := 10; if you want to see what Maple is doing behind the scenes when you give it a command. If you want to see more, use printlevel := 50 or higher. Often by inspecting the output when printlevel is greater than 1 (the default), you can discover what is ailing your worksheet.

Use debug. If you have defined a word, say `something` and it does not do what you want, you can often discover the error by typing debug(something); in an input cell and pressing the enter key. When you use the word again, its behind the scene computations are printed out for your inspection.

Want to see a word definition? Say you want to see how plot works. Type interface(verboseproc=2); in an input cell and press enter. Then type print(plot);