Setting Up and Solving Problems

 For our purposes, a problem is anything that can be formulated as a question whose answer involves some mathematics.  The main use of mathematics is to solve problems, and the best way to learn mathematics is to solve problems.  This idea of a problem includes the 'skill' exercises that are always at the end of the sections in mathematics textbooks.  For example, early in beginning algebra there is a section on solving linear equations, and at the end of that section there is a set of exercises consisting of lots of problems like 'solve      for x'.

It also includes 'word problems' which can be solved using the methods mastered in the skill exercises.  The word problems often are stated at the beginning of the section as motivation for the methods which are developed in the section.  Problems usually arise in a context.  Once the context is well understood, the problem can be formulated or posed and a method of solution worked out.  From this solution, other problems may arise which require solving.  We want to consider this problem identification and formulation as part of problem solving also.

The process of solving a problem is an active process, but can get bogged down for lack of knowing what to do next.  So it is helpful to have a list of things to do.  Here is one list of steps to carry out when you are solving a problem.

  SETUP the problem.   This involves several steps.

•  Pose/Read   the problem carefully, getting straight the meaning of all the terms used in the statement.
• Draw a picture or diagram.  This is a good way to focus thoughts, and gives you a place to put your labels.
• Label or list the dimensions (or variables) important to the problem.  Among these are the given dimensions, that is, the dimensions whose values are stated in the problem, the requested dimensions, that is, the dimensions whose values are requested in theproblem, and the intermediate dimensions, that is, the dimensions which arise in the process of trying to determine the requested dimensions from the given dimensions.
•  List or derive the equations relating the labeled dimensions.

SOLVE the equations we have set up for the required dimensions in terms of the given dimensions. This is one of places where Maple comes in very handy.   It is   easy to get bogged down in the calculations so that you lose all interest in solving the problem. This is less likely to happen if you have Maple at your disposal.

INTERPRET the obtained solutions .  What are the realistic solutions given the context of the problem?  Which should be ignored?  Have all solutions been obtained?

 Where does Maple come in handy in this process?  In the Solve phase, mostly.  The actual setting up of the problem as a mathematical problem has to be done by you.  Regard Maple as a tool to carry out and record the solution you imagine.  A very important word in the Maple vocabulary is solve .    This word is used to solve a system of one or more equations which come up.

 Problem: A swimming pool is three times as long as it is wide.  It is also 40 feet longer than it is wide.  Find its dimensions.

Solution :  Let l and w be the length and width of the pool. Then the first statement of the problem translates to the equation   l = 3w , and the second statement to   l = w + 40 .  We need to solve these two equations simultaneously for l and w.  First, set up the equations.

>	eq1 := l = 3*w;

>	eq2 := l = w + 40;

>

Then solve the system for l and w.  We can do this by subtracting eq2 from eq1 and solving for w, getting   w = 20 , then substituting that value for w into eq1 getting   l = 60 .

>	eq3 := eq1 - eq2;

>	eq4 := lhs(eq3) - 2*w = rhs(eq3) - 2*w;

>	eq5 := -(1/2)*eq4;

>	eq6 := subs(eq5,eq1);

>	solution := {eq5,eq6};

>

>	solve({eq1,eq2},{l,w});

>

The pool is 20 feet wide and 60 feet long.

The word solve is a very good to know, but it is not infallible.  It uses some methods of solving equations which you know and some which you probably don't know.  Don't give up just because solve doesn't give you a solution.

 So it is important to also be able to solve equations by various means.   Here are four.

Guess and check.   This method involves  guestimating a solution somehow  and checking your accuracy somehow.  For example, suppose you had guestimated that the dimensions of the pool are about 25 by 55 feet and wanted to check that.  Use the word subs .    

>	subs({w=25,l=75},[eq1,eq2]);

>

This line says to substitute 25 and 75 for w and l in eq1 and eq2.

(Notice the use of braces and brackets here.  Braces  are used to enclose the members of a set and brackets are used to enclose the members of a list.  In a set, the order is not important and repetitions are not counted; in a list, the order is important and repetitions are counted.)  As we can clearly see, our guestimate is off.  We have satisfied the first equation, but not the second.  If we decrease the value of w by 1, then we have to decrease the value of l by 3 in order to continue to satisfy the first equation.  Will we come closer to satisfying the second? Let's see.

>	subs({w=24,l=72},[eq1,eq2]);

>

Well, yes, if ever so slightly.  The left-hand side of the second equation has decreased by 2 towards the right-hand side.  We could pursue this method of guessing and then trying to improve our guess, but let's put that off until later.

  By Hand, as with pencil and paper.  

You can choose to try to solve your equations by hand  by which I mean to manipulate the equations the same way you would do using pencil and paper.  This can be done without using solve at all.  This is what we did in our original solution to the swimming pool problem.  On the other hand, we could simplfy the equations and then use the word solve.   For example, let's solve the two equations, eq1 and eq2, by hand.  Using the Maple word solve we need only solve one equation for one unknown.   Here is a possible way to proceed:

>	eq3 := subs(l=solve(eq1,l),eq2);

>	sol1 := w = solve(eq3,w);

>	sol2 := l = solve(subs(sol1,eq1),l);

>	sol := {sol1, sol2};

>

  Graphical solution.  

Another way to solve equations is graphically.  Here we can plot each equation, using plot or implicitplot and use the pointer to locate the approximate solutions.  These solution(s) are the located where the graphs of the equations coincide.  Note:  the word implicitplot can only be found in Maple V Release 2.  Earlier versions of Maple only plot functions.  This method also works very well on a graphing calculator.

>	with(plots):

>	implicitplot({eq1,eq2},w=10..30,l=50..70);

>

>

  Using  fsolve.  

Another way to solve equations is with   fsolve .  This word employs methods of calculus to find floating point approximations to the equation you are trying to solve.  If you do not supply fsolve with an interval in which to search for a solution, then it returns the first solution it finds.  This word works well in conjunction with   plot .  You can use plot to narrow down the search interval, and then use fsolve to get the 'exact' answer.

 A. Solve  the following systems of equations.

1.     ,      

>

>

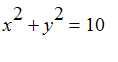2.    .

>

>

3. 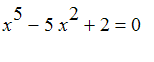       use plot and fsolve here.

>

>

4.       for  and .

>

>

B. Solve the following word problems by setting up and solving a system of equations.

1.  The height of the Eiffel Tower in Paris is 125 feet less than twice the height of the Washington Monument.  The latter is 75 higher than the Great Pyramid of Cheops and 105 feet higher than the dome of St. Peter's Church in Rome.  If the sum of the heights of these four edifices is 2510 feet, find the height of each to the nearest foot.

>

>

2.  A large conference table is to be constructed in the shape of a rectangle with two semicircles at the ends (see figure).  Find the dimensions of the table, given that the area of the rectangular portion is to be twice the sum of the areas of the circular ends, and the perimeter of the whole table is to be 40 feet.

Here is a diagram to accompany the problem.

>	F:=plot([-cos(t)+1,sin(t)+1,t=Pi/2..-Pi/2]):

>	G:=plot([cos(t)+6,sin(t)+1,t=Pi/2..-Pi/2]):

>	H:=plot([[1,0],[6,0],[6,2],[1,2],[1,0]],style=LINE):

>	plots[display]({F,G,H},axes=none,scaling=constrained);

>

>

3.  A local hardware store worker is making up a fertilizer mix from some left over fertilizer from the summer.  There are three types, with 30 percent, 20 percent and 15 percent  nitrogen content respectively.  When he mixed all the fertilizers together and tested the nitrogen content, he found that the mix weighed 600 pounds and contained 25 percent nitrogen content.  How many pounds of each type did he have left over?  How many solutions does this problem have?

>

>

4.  A 30 foot ladder and a 40 foot ladder are positioned so as to cross each other in an alley.  That is, they are leaning up against opposite walls with their bases snug up against the base of the opposite walls.  Given that they cross at a point 10 feet above the floor of the alley, determine the width of the alley.

>

>

5.  Make up your own algebra problem to set up and solve using Maple.  It can be a variation on one of the problems above, or it can be something entirely different.

>

>

>	with(plots);

We have already used   plot ,   implicitplot , and   display  (in problem 2 of part B).  To learn more about these very useful commands simply type

>

?plot

>	?implicitplot

>

?display

>

?textplot

>

?animate

>

or anything else that might interest you.  Look at the bottom of the help files for examples.  Sometimes, you are your best teacher.  Learn by experimenting with a few (or all) of these commands.  Also, you will learn more about these words in worksheets to come.

Parameterized Swimming Pool Problem  

Problem:   swimming pool is p times as long as it is wide.  It is also 40 feet longer than it is wide.  What are its dimensions in terms of p?  Describe how the dimensions vary with p.

Solution:   We could just go back to the cell containing the original equations and put in a p for 3 in eq1.

>

restart;

The word    restart     clears all variables by rebooting Maple.

>

p := 'p';

>	eq1 := l = p*w;

>	eq2 := l = w + 40;

>

Now we would solve for l and w, just as before, except now the solution is given in terms of the parameter p.

>	sol := solve({eq1,eq2},{l,w});

>

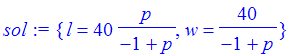
Now by inspection, we can see that as p gets large, both w and l get small.  Also, as p approaches 1 from the left, l and w get large.  In more complicated situations, we could use plot to study how the solution changes as the parameter changes.

>	plots[animate]({p*w,w+40},w=0..80,p=0..2);

>

1.  What happens to the solution to the swimming pool problem as the difference of the width and length is allowed to vary?  (Keep the ratio of the width to the length constant.)

>

>

2.  A large conference table is to be constructed in the shape of a rectangle with two semicircles at the ends (see figure).  Find the dimensions of the table, given that the area of the rectangular portion is to be p times the sum of the areas of the circular ends, and the perimeter of the whole table is to be 40 feet.

>

>

>

3.  Study the solution to the mixture problem, no.3, in the previous problem set.  Vary a parameter of your choice and describe how the solution changes.

>

>

4.  A 30 foot ladder and a 40 foot ladder are positioned so as to cross each other in an alley.  That is, they are leaning up against opposite walls with their bases snug up against the base of the opposite walls.  Given that they cross at a point h feet above the floor of the alley, determine the width of the alley.

>

>

This is a good place to learn how to develop and define Maple words in a worksheet.  The idea is very simple:

    A.  Name the given quantities --

As you are solving a problem or developing an algorithm, assign the given quantities to appropriate names which you have chosen. Put these assignments into a single input cell, which we will call the parameter cell.

    B.  Compute the desired quantity --  

Use the names assigned in your maple statements which you make in your algorithm.  This part will change and grow as you develop the definition, but try to keep all the statements in one input cell, which we will call the definition cell.  Once you get the desired output,

    C.  Make the Definition --

This involves mostly choosing a name for the procedure, inserting it at the top of the definition cell in the line
 

      name := proc(p1,p2,...,pn)     

which begins the definition by assigning the name and declaring the input parameters p1,  p2, etc.  

At the bottom of the definition cell is the word

      end;     

which signals the end of the definition.

Now, when you execute the definition cell, you should get a nicely formatted version of the definition as output.   

This is not the only set of steps you could follow when developing a definition, but it is very natural one and works well for small definitions.

Copy all of the input cells used to obtain the solution into one input cell.

 Then all we need to do to define the word is to insert a proc line at the top and an end at the bottom.  

When inserting the proc line, you must decide what the inputs      for the word will be.   We will let the ratio of the length of the pool to the width of the  pool be the only input in this word.  We were calling that p in the equations, so use the same name in the proc line.

>	swim := proc(p)

>	eq1 := l = p*w;

>	eq2 := l = w + 40;

>	sol := solve({eq1,eq2},{l,w});

>

end;

Warning, `eq1` is implicitly declared local

Warning, `eq2` is implicitly declared local

Warning, `sol` is implicitly declared local

>

When you execute the input cell containing the definition, the word   swim  has been added to the vocabulary and can be used like any other Maple word.   The assignments made in the definition are declared local and a warning is issued unless you declare the names either local or global .     Usually, you will want any assignments to be local,  just in case you are using the same name outside the word to mean something else.

The output from a word is the output from the last line before the end line.  So, for example,  if the pool is 3 times as long as it is wide then p = 3 and we would say

>

swim(3);

On the other hand, if we put in a ridiculous input  what would happen?

>

swim(-4);

>

You can redefine the word if there is something that needs changed.  For example, the swimming pool problem doesn't really have a solution if p is not positive, so we could insert an error trap     here.

>	swim := proc(p)

>	if not type(p,name) and not p > 0 then ERROR(`oops`)

>	else       eq1 := l = p*w;

>	eq2 := l = w + 40;

>	sol := solve({eq1,eq2},{l,w});

>

fi

>

end;

Warning, `eq1` is implicitly declared local

Warning, `eq2` is implicitly declared local

Warning, `sol` is implicitly declared local

>

Now redefine swim and check --

>

swim(-4);

Error, (in swim) oops

>

Usually,  one doesn't spend a great deal of time inserting error traps in word definitionst.  There are much more interesting things to do with the mathematics of the situation.  For example,  suppose we wanted to change the inputs to allow for changing the 40,  the amount the length exceeds the width, that occurs in the  problem.   Then simply copy down the definition into a new input cell and make the appropriate changes.   Something like this will work:

>

restart;

>	swim := proc (p,excess) local eq1, eq2, sol;  eq1 := l = p*w; eq2 := l = w+excess; sol := solve({eq1, eq2},{l, w})  end;

>	swim(3,40);

>	swim(3,ex);

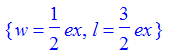
Notice that  you can 'read off' the solution in words if you put in a variable for the excess.  So, if  the pool is 3 times as long as it is wide, then the width must be 1/2 of the excess and the length is 3/2 of the excess.

You can also define a word  to draw a picture of  the pool.  These types of words are very useful to perform a visual check of computations.  Sometimes, you have solved a problem incorrectly, but do not discover that until you have performed a visual check on the solution you have obtained.

To develop a visual check of our swimming pool problem, we can first draw one picture.  Get the dimensions of a pool

>	dims := swim(3,40);

Now we want to draw a rectangle which is 20 by 60.  We can set up a general rectangle  with one corner at  the origin and the opposite corner at [l,w]

>	rect := [[0,0],[l,0],[l,w],[0,w]];

>	pool := subs(dims,rect);

>	plots[polygonplot](pool, color=blue,style=patch, scaling = constrained);

Now we can define the word.  Copy down and join the appropriate input cells. Then  insert a proc line at the top (deciding on what the inputs will be), and an end line at the bottom of the new input cell.

>	drawpool := proc(p,excess) dims := swim(p,excess); rect := [[0,0],[l,0],[l,w],[0,w]];

>	pool := subs(dims,rect);

>	plots[polygonplot](pool, color=blue,style=patch, scaling = constrained); end;

Warning, `dims` is implicitly declared local

Warning, `rect` is implicitly declared local

Warning, `pool` is implicitly declared local

>	drawpool(3,40);

>	movie := [seq(drawpool(3,10*i),i=1..8)]:

>	plots[display](movie,insequence=true);

>

Exercise:  Make a movie of the change in the pool as the ratio p changes from 1 to 4 by increments of 1/2.

>

>

Exercise:  What is wrong with taking the original word swim and changing to proc line to read  swim := proc(p,w) ?

>

>

Exercise:  Modify  drawpool so that if the ratio p is greater than 2, the color of the pool is blue, otherwise the color is red.

>

>

 Exercise:  Define a word   quadform  to take three numbers a, b, c and return the roots of the quadratic equation 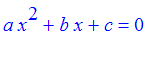  , if they are real, and the message 'no real roots' if they are complex.   Don't just use solve here .

>

>

Exercise:   Modify the word swim so that it simply returns the point [l,w] rather than the solution to the equations.

>

>

Exercise:   Define a word which takes a function and tabulates its value over a given interval with a given increment between x values.

>

>