![[Maple Plot]](images/hand61.gif)
More Max-min Problems
Stumbling onto max-min Problems
Sometimes, in the process of working on one problem, which may not be a max-min problem at all, one may stumble onto an interesting max-min problem. This can occur naturally in a Maple worksheet. Just take a problem in which you need to calculate a quantity in terms of some given quantities. Then make one of the given quantities a variable quantity and go through the calculation. At the end, you have obtained a formula expressing the desired quantity as a function of the variable quantity. Then you can study the behavior of this function with plot and diff, locating any extreme values it may possess. Here is an example.
A Ladder Problem: A 20 foot ladder is leaning against the top corner of a bay window in such a way that the top of the ladder is just resting against the wall of the house, and the base of the ladder is on the ground. The top corner of the window is 3 feet out from the house and 12 above the ground. How high up on the wall is the top of the ladder touching?
| > | restart; |
| > | with(plots): |
| > | A1:=plot({[[0,15],[0,-1]],[[0,12],[3,12],[3,4],[0,4]]},color=navy): |
| > | A2:=plot({[[-1,0],[16,0]],[[0,14.937],[15.257,0]]},color=black): |
| > | A3:=textplot({[-.5,13,'h'],[8,8,'d'],[-.75,6,`12`],[1.5,11.25,`3`]}): |
| > | display({A1,A2,A3},axes=none,scaling=constrained,style=line); |
![[Maple Plot]](images/hand61.gif)
| > |
Solution:
Let's parameterize this problem by changing the length of the ladder to a parameter, say d. If we set up a coordinate system so that the wall is the positive y-axis, the ground is the positive x-axis, and the corner of the bay window is at (3,12), then by similar triangles, h/sqrt(h^2+3^2) = (h+12)/d , where h+12 is the height above the ground the ladder touches the wall. Let's let Maple do some work. First set up the equation and simplify it.
| > | restart; |
| > | eq := h^2/(h^2+9) - (h+12)^2/d^2; |
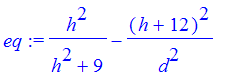
| > |
Let's manipulate eq a little.
| > | eq := (collect(numer(normal(eq)),h)); |
![]()
| > |
If we solve for the height above the wall, h, in terms of the length of the ladder, d, we get more extraneous solutions than if we solve eq for d in terms of h.
| > | sol := [solve(eq,d)]; |
![sol := [(h^2+9)^(1/2)*(h+12)/h, -(h^2+9)^(1/2)*(h+12)/h]](images/hand64.gif)
| > |
Clearly, we are interested in the positive values for d, ie,
![]() .
.
| > | plot(sol[1],h=3..7); |
![[Maple Plot]](images/hand66.gif)
| > |
Upon examination of the graph, we see that there are two solutions to the original problem. In fact, and this is clear if we reflect on the situation, there will generally be two positions the ladder can occupy if it is long enough, no positions if it is too short, and exactly one position if the ladder exactly the right length. That length is slightly under 20 feet, the y-coordinate of the base of the graph. We can discover this length easily.
| > | hmin := fsolve(diff(sol[1],h),h,4..5); |
![]()
This gives the height above the bay window that the ladder touches.
| > | dmin := subs(h=hmin,sol[1]); |
![]()
| > |
So, we have stumbled onto the solution of the problem of finding the shortest ladder such that there is a solution to the problem.
Wandering Critical Points:
For the cubic
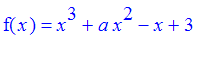 , plot in the same window the graphs of f for several positive values of a. What happens to the local extreme points and the inflection points of f as a increases from 0 towards infinity? Also, try to use the word animate to do the same thing.
, plot in the same window the graphs of f for several positive values of a. What happens to the local extreme points and the inflection points of f as a increases from 0 towards infinity? Also, try to use the word animate to do the same thing.
| > | plots[animate](x^3+a*x^2-x+3,x=-12..9,a=0..10,color=blue); |
![[Maple Plot]](images/hand610.gif)
| > |
Asymptotes
Make a sketch of the function
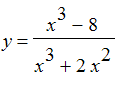 . Find all asymptotes of the function. Also, find the intercepts, the local maxima, local minima, and inflection points of the function.
. Find all asymptotes of the function. Also, find the intercepts, the local maxima, local minima, and inflection points of the function.
| > |
| > |
T wo Pigpen problems
Pigpen I: A pigpen (shed for holding pigs) is to be shaped like a box with no floor and no front. The top is to be square, and the volume is to be 18 cubic yards. What dimensions should the pigpen have in order to minimize the amount of material used to construct it?
| > |
| > |
Pigpen II: Instead of requiring the top to be square, suppose we want the top to be b times as wide as it is long, where b is some fixed positive number. Find the minimum amount, A, of material needed to construct such a pigpen as a function of b. Draw a conclusion about the most economical shape for the top of the pigpen.
| > |
| > |
Big Clock Problems
Big Clock I: A tower clock has a 4 foot minute hand and a 3 foot hour hand. How fast are the tips of the hands moving apart at 12:15?
| > |
| > |
Big Clock II: At what time are the hands moving apart most quickly?
| > |
| > |
Wandering points
Define the function and compute its derivatives.
| > | restart; |
| > | f:= x -> x^3 + a*x^2 - x + 3; |
![]()
| > | fp := unapply(diff(f(x),x),x); |
![]()
| > | fpp := unapply(diff(f(x),x,x),x); |
![]()
| > |
Let's plot f over x from -6 to 4 and a from 0 to 5.
| > | plot({seq(f(x),a=0..5)},x=-6..4); a := 'a': |
![[Maple Plot]](images/hand615.gif)
| > |
Looking at the graphs suggests that the local maximum (the leftmost critical point) wanders off to the left and drifts upward. The other critical point and the inflection point seem to stay stationary, although that may be an illusion. Let's calculate the points and look at their limits as a goes to infinity. First, find the x-coordinates of the critical points and the inflection point.
| > | cp := solve(fp(x),x); |
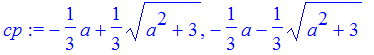
| > | ip := solve(fpp(x),x); |
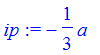
| > |
We can see that as a gets large,
![]() and
and
![]() go to 0 and
go to 0 and
![]() , respectively.
, respectively.
| > | limit(cp[1],a=infinity); |
![]()
| > | limit(cp[2],a=infinity); |
![]()
| > |
The local minimum of
![]() as a approaches
as a approaches
![]() is (0,3), and the local maximum and inflection points head towards (
is (0,3), and the local maximum and inflection points head towards (
![]() ), with the inflection point roughly halfway between the two extrema.
), with the inflection point roughly halfway between the two extrema.
To observe the graph of
![]() as increases (for example, from
as increases (for example, from
![]() to
to
![]() ) is a great problem for using the word animate. Here is a sample of what you might have done. Once you have activated the animate plot press your pointer on the 'once' button to make the animate plot 'loop'.
) is a great problem for using the word animate. Here is a sample of what you might have done. Once you have activated the animate plot press your pointer on the 'once' button to make the animate plot 'loop'.
| > | plots[animate](x^3+a*x^2-x+3,x=-12..9,a=0..10,color=blue); |
![[Maple Plot]](images/hand629.gif)
| > |
Pig Pen II
First draw a picture
| > | A1:=plot({[[0,0],[0,2],[2,3],[5,3],[5,1],[3,0], [3,2],[0,2]],[[0,0],[3,0],[3,2],[5,3]]},color=navy): |
| > | A2:=plots[textplot]({[1.5,-.25,'w'],[4.25,.35,'l'], [5.25,2,'h']},color=black): |
| > | A3:=plots[textplot]([2,3.25,`No front, no floor`],color=black): |
| > | display({A1,A2,A3},axes=none,scaling=constrained); |
![[Maple Plot]](images/hand630.gif)
| > |
We are given that the length I of the pen is bw, where b is a fixed positive number. The problem is to minimize the area,
![]() , of the pen subject to the constraint that the volume, V=hlw , of the pen is 18 cubic feet.
, of the pen subject to the constraint that the volume, V=hlw , of the pen is 18 cubic feet.
| > | restart; |
| > | A := 2*h*l + h*w + l*w; |
![]()
| > | l := b*w; |
![]()
| > |
Now the area is expressed as a function of the height and width of the pen. But the height of the pen is h = 18/(lw) from the constraint equation. Let's substitute for h and turn A into a function.
| > | A := unapply(subs(h=18/(l*w),A),(b,w)); |
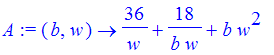
| > |
Plotting the area function for various values of b
| > | plot({A(1,w),A(1/2,w),A(1/10,w)},w=1..15); |
![[Maple Plot]](images/hand635.gif)
| > | plot(A(1/2,w),w=1..15); |
![[Maple Plot]](images/hand636.gif)
| > |
'might' lead one to suspect that the minimum of the minimums
![]() occurs at
occurs at
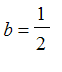 . We can express
. We can express
![]() as a function of b. First, find the width
as a function of b. First, find the width
![]() of the pen with minimum area. That will occur at the real root of
of the pen with minimum area. That will occur at the real root of
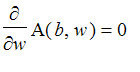 . Then substitute that in for w in A.
. Then substitute that in for w in A.
| > | Aw := normal(diff(A(b,w),w)); |
| > | w[b] := ((9+18*b)/b^2)^(1/3); |
| > | A[b] := unapply(A(b,w[b]),b); |
| > | fsolve(diff(A[b](b),b),b,0..1); |
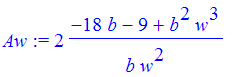
![w[b] := ((9+18*b)/b^2)^(1/3)](images/hand643.gif)
![A[b] := proc (b) options operator, arrow; 36/((9+18*b)/b^2)^(1/3)+18/b/((9+18*b)/b^2)^(1/3)+b*((9+18*b)/b^2)^(2/3) end proc](images/hand644.gif)
![]()
| > |
Indeed, our suspicion pans out.
Big Clock II .
By the law of cosines, the distance s between the tips of the minute hand and the hour hand is
| > | restart; |
| > | s := sqrt(3^2+4^2 - 2*3*4*cos(theta)); |
![]()
| > |
where
![]() is the angle between the hands. This angle is a linear function of time t measured in minutes. At
is the angle between the hands. This angle is a linear function of time t measured in minutes. At
![]() the angle is 0 radians and after
the angle is 0 radians and after
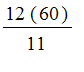 minutes the angle is
minutes the angle is
![]() radians, so in general,
radians, so in general,
| > | theta := (11/12)*(2*Pi/60)*t; |
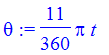
| > |
To find when the distance between the minute hand and hour hand is increasing most rapidly, lets think through what happens. At 12:00, the hands are together, but the minute hand is moving away from the hour hand. Actually they are both moving to the right, but the minute hand moves 12 times faster. The time at which the distance between the two hands are increasing most rapidly would be when the second derivative of s with respect to time is zero. This will occur sometime before the hands are pointing in opposite directions, which works out to be
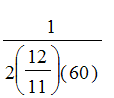 minutes past 12.
minutes past 12.
| > | sp := diff(s,t); |
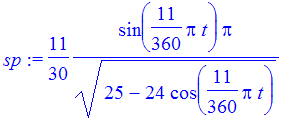
| > | spp := normal(diff(sp,t)); |
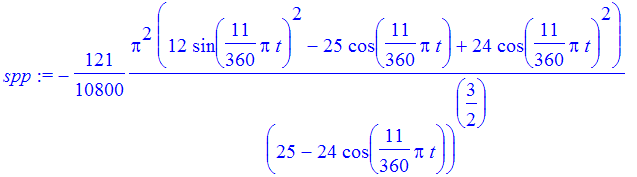
| > | ti := fsolve(spp,t,0..30*12/11); |
![]()
| > | evalf(subs(t=ti,sp)); |
![]()
| > | evalf(subs(t=ti,s)); |
![]()
| > |
| > |
So at about 7.529 minutes after 12, the distance between the tips of the minute hand and the hour hand is increasing at the maximum rate of about .288 feet per minute. Also, the tips are about 2.65 feet apart at that time.