The theorems of Calculus up to the fundamental theorem  fit into the  nice logical sequence  given below.   The following diagram gives a partial picture of how the theorems are related.

[Limdef] Definition of Limit.   Let a be a number and let f be a function defined at least on an open interval which contains a or has a as an endpoint. The limit of f at a is L means that for any positive number  there is a positive number  such that for each number x at which f is defined and which is within  of a (but different from a ), f(x) is within  of L .

       [Limprps]

  Sum and Product of Limits .  If each of two functions have a limit at a point, then so does their sum, difference, and product; in fact, the limit of the sum (difference, product) is the sum (difference, product) of the limits. Also the limit of the quotient is the quotient of the limits, provided the limit of the denominator is not 0.  

Hint on proof: Use the definition of limit to prove these properties.

  The Squeeze Theorem .  If each of two functions has the same limit at a point, and a third function is squeezed between them, then it also has that limit at the point.

Hint on proof: Use the definition of limit.

[Condef]  Definition of continuous function.  A function is continuous at a point if it is defined there and its value there is its limit there. A function is continuous if it is continuous at each point where it is defined.

[Contprps] Sum, Product, of Continuous Functions.  The sum (difference, product) of two continuous functions is continuous, at each point where they are both defined. The quotient of two continuous functions is continuous at each point where they are both defined and the denominator is not 0. The composition of two continuous functions is continuous at each point where it is defined.

Hint on proof: Use SPLT.

 [Derdef] Definition of Derivative.  A function f is differentiable at a provided it is defined at a and the limit of 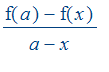   at a exists. The derivative f is the function    whose value at a is the above limit, if it exists.

[RULD] Rules for Derivatives.  The derivative of a constant function is the constant function 0. The derivative of the sum (difference) of two functions is the sum (difference) of their derivatives. The derivative of the product of two functions is the derivative of the first times the second plus the first times the derivative of the second. The derivative of the quotient of two functions is the quotient of the derivative of the top times the derivative of the bottom minus the top times the derivative of the bottom with the square of the bottom. The derivative of the composition of two functions is the derivative of the first composed with the second times the derivative of the second.

Hint on proof: Use the definition of derivative.

[DIC ] Differentiability Implies Continuity.  If a function is differentiable at a point, then it is continuous at that point.

Hint on Proof:  Use the definitions.

  [IV] Intermediate Value Theorem.  If a function is continuous on an interval,then each number between two values of the function is itself a value of the function.

Hint on proof: You need the least upper bound property to prove this theorem.

[EXV1] Extreme Value I.  If a function is continuous on a closed interval, then it has both a minimum value and a maximum value somewhere in the interval.

  Hint on Proof: You need the least upper bound property to prove this theorem.

[EXV2] Extreme Value II .   If a function is continuous on a closed interval, then its extreme values on the interval occur at the endpoints of the interval or at the places interior to the interval where the derivative is 0 or not defined.

Hint on Proof:  Use the definition of continuous function.

[ROLL] Rolle's Theorem .  If a function is continuous on a closed interval, differentiable at each point inside the interval, and has the same value at the endpoints of the interval, then its derivative is 0 at some point inside the interval.

Hint on Proof:  Use the extreme value theorems.

[MVT] Mean Value Theorem.  If a function is continuous on a closed interval and differentiable at each point inside the interval, then at some point inside the interval the derivative is equal to the average change in the function over the interval.

Hint on Proof:  Use Rolle's Theorem.

[FST] First Sign Theorem.  If the derivative of a function is positive (negative) at each point in an interval, then the function is increasing (decreasing) over the interval.

Hint on Proof:  Use the Mean Value Theorem.

[FDT] First Derivative Test.  If the sign of the first derivative changes from positive to negative (negative to positive) across a critical point, then the function has a local maximum value (local minimum value) at the critical point.

Hint on Proof:  Use the first sign theorem.

[SST] Second Sign Theorem.  If the second derivative of a function is positive (negative) on an interval , then the function is concave up (down) on that interval.  

Hint on Proof:  Use the Mean Value Theorem.

[SDT] Second Derivative Test.  If the second derivative of a function is positive (negative) at a critical point of the function, then the function has a local minimum (maximum) at the point. No conclusion may be drawn if the second derivative is 0 at the critical point.

 Hint on Proof:  Use the second sign theorem.

 Definition of Antiderivative.  A function F is called an antiderivative of a function f provided the derivative of F is f .

[TOA] Theorem on Antiderivatives.  If two functions have the same derivative on an interval then they differ by a constant function on that interval.

Hint on Proof:  The proof of this theorem uses the Mean Value Theorem.

 Definition of Integral.  Let f be defined on [a,b] . A partition  of [a,b] is a finite set of points in [a,b] ,  for  from 0 to n.        is a subinterval of the partition. The mesh of the partition is the width of the longest subinterval of the partition. A Riemann Sum of f over the partition  is a number     where each is chosen from the subinterval    .The integral of f over [a,b] is the number L such that for any positive number  , there is a positive number  such that each Riemann Sum of f over each partition of mesh less than  is within  of L , provided such a numberL exists.

[FET] First Evaluation Theorem.  The integral of a constant function over an interval is the constant times the width of the interval.

 Hint on Proof:  Use the definition of the integral.

[LPR] Linearity Property.  The sum of two functions, each integrable over an interval, is itself integrable over the interval, and the integral of the sum is the sum of the integrals. The integral of a constant times a function is the constant times the integral of the function.

 Hint on Proof:  Use the definition of integral.

[APR] Additivity Property.  If a function is integrable over an interval, and the interval is partitioned into two subintervals, then the integral of the function over the entire interval is the sum of the integrals of the function over the subintervals.

Hint on Proof:  Use the definition of integral.

[CPR]   Comparison Property.  If the graph of one function never goes above the graph of a second function, then the integral of the first function does not exceed the integral of the second function.  

Hint on Proof:  Use the definition of integral.

[CIT] Continuity Implies Integrability.  If a function is continuous on an interval, then it is integrable over the interval.

Hint on Proof: The proof of this theorem requires the least upper bound property of the real numbers.

[PPR] Positivity Property.  If a function is continuous and non-negative on an interval, and takes on a positive value, then its integral over the interval is positive.

Hint on Proof: Use the comparison property and the definition of continuous function.

[IMV] Integral Mean Value Theorem.  If a function is continuous on an interval, then the value of its integral over the interval is the value of the function someplace in the interval times the width of the interval.

Hint on Proof:  The proof of the integral mean value theorem uses the first extreme value theorem, the first evaluation theorem, the comparison property, and the intermediate value theorem.

[FUND] Fundamental Theorem.  If a function is continuous on an interval, then  (i) (existence) it has an antiderivative on the interval; in fact, the function F defined on [a,b] by the formula F(x) = the integral of f over the interval [a,x] is an antiderivative of f on [a,b] .Furthermore, (ii) (Evaluation) the integral of the function over the interval is obtained by taking any antiderivative of the function, and subtracting its value at the left-hand endpoint from its value at the right-hand endpoint.

Hint on Proof:  To prove (i), use the integral mean value theorem. To prove (ii), use (i) and the theorem on antiderivatives above.