Locus Problem.

Let ABC be a triangle constrained to move in the plane so that its vertices A and B always lie on a pair and of intersecting lines so that if A is on one line then B is on the other. Show that the locus of the point C is an ellipse.

A Solution.

Without loss of generality, assume that the lines are the x and y axes, and that the length of side AB is 1. Parameterize the point A as [t,0], where t ranges between -1 and 1. The point B takes two positions and . Now the point C = [x,y] can be written as

C = s*A + (1-s)*B + r*perp(A-B),

where s and r are fixed numbers, and perp(A-B) is the vector A-B rotated 90 degrees counterclockwise (so if B = then perp(A-B) = and if B = then perp(A-B) = ).

To show that C traces out an ellipse, write parametric equations for C and eliminate the parameter:

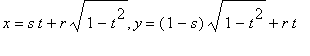
Case 1 .

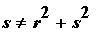
To eliminate the parameter, solve the equations for t and 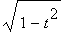, and substitute those values into the equation .

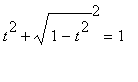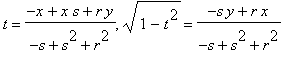
Making the substitution, we get

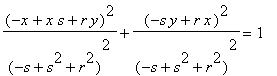
This quadratic equation in x and y graphs an ellipse (since it is not a hyperbola or parabola). Below is a typical locus where r = 2 and s = 1. Note that the foci have been inserted. See below for the computation.

Here is a locus where the the "triangle" ABC is a segement: r = 0, s = 1.5

To compute the foci of the ellipse, note that the ellipse 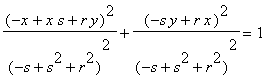is the image of the circle 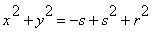under the linear transformation defined by the matrix

The eigenvectors and eigenvalues of A are 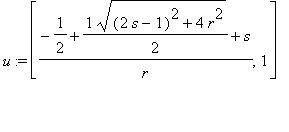, , 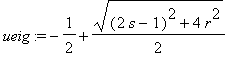and

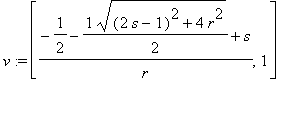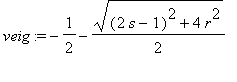, . Since A is symmetric, we know the eigenvectors are perdicular and form the principal axes of the ellipse. The eigenvalues (in absolute value) are the major semi-axis in the director of v and minor semi-axis 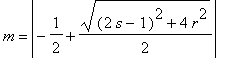in the direction of u. So the foci are and .

Note that the ellipse is a circle exactly when 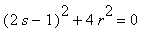, that is, when s = 1/2 and r = 0; geometrically, this says the only time the trace of C is a circle is when C is the midpoint of the segment AB. Here is the locus at that point.

Case 2.

At time t =1, the vertex C is at [s,r] and the segment AB is the unit segment [[0,0],[1,0]]. Note the point [s,r] is on the circle of radius 1/2 centered at [1/2,0] and so the triangle ABC is a right triangle with the vertex C opposite the hypotenuse. We can eliminate here the parameter t by multiplying x by r and y by s and subtracting, to get 0. So the vertex C traces out a segment on the line y = x. With a little more work, one could show this segment to be a diameter of the unit circle.

Here is an animation showing the trace of C in magenta for all the exceptional values for r and s.

Maple computations