A Polar problem

Start with a circle c and a point P (outside c). Draw the two tangents from P to c passing through points Q and R (on c). Call the line through Q and R the polar of P and c. . Now take any point X (outside c) on the polar of P and c. Then the polar of X and c passes through P.

Solution:

Need a Lemma. If 0 < t < 1, then the line through P = and Q = is orthogonal to the radius of the unit circle drawn to Q.

Proof: Compute that Q dot P-Q = 0. QED

> restart;assume(t>0,t<1);

> P := t->[1/t, 0]; Q := t->[t, sqrt(1-t^2)];

> linalg[dotprod](Q(t),(P-Q)(t));

>

Note that if P is thought of as a complex number, then 1/conjugate(P) = [t,0] is on the polar of P and c, which is in fact perpendicular to the line passing through 0 and P. If we multiply everything in the picture by a complex unit, then P goes to an arbitrary point X outside of c and the polar to P, 1/conjugate(P) goes to 1/conjugate(X), and the polar of P and c goes to the polar of X and c. So we get a

Corollary . If X is any complex number outside the unit circle c, then the polar of X and c is the perpendicular to the line through 0 and X which passes through 1/conjugate(X).

So, on to the solution.

Coordinatize so that c is the unit circle and P = [1/t,0], with 0 < t < 1. Then WLOG, take

Q = and R = . By the lemma, the line through Q and R is the polar of P. Now let where r > 0. By the corollary, the polar of X and c is the line through 1/conjugate(X) which is perpendicular to the line through [0,0] and X. Consequently, it suffices to show that the line through 1/conjugate(X) and P is perpendicular to the line through [0,0] and X. That is, show X dot (P-1/conjugate(X)) = 0.

> additionally(r>0);

> X := t -> t+(sqrt(1-t^2)+r)*I;

> rcX:=evalc(1/conjugate(X(t)));

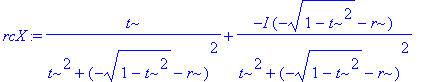
> linalg[dotprod]([Re(X(t)),Im(X(t))],P(t)-[Re(rcX),Im(rcX)]);

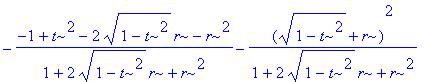
> simplify(%);

Done. QED

Now for a picture.

First, draw the circle.

> c := plot([cos(t),sin(t),t=0..2*Pi],color=blue,thickness=2):

Now define the point R mentioned in the problem.

> R := t-> [t, -sqrt(1-t^2)];

Redefine X and 1/conjugate(X) so that they return [a,b] instead of a + b*I

> X := (t,r) -> [t, sqrt(1-t^2)+r];

> rcX := unapply([Re(rcX),Im(rcX)],(t,r));

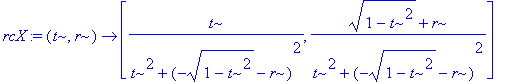
It will be useful to compute the points S and T where the polar of X and c meets c. Note that they are

the two points of the form s*X + (1-s)*P which are on c.

> Y:=evalm(s*rcX(t,r)+(1-s)*P(t));

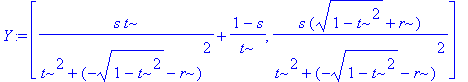
> solve(Y[1]^2+Y[2]^2=1,s):

> sol:=simplify([%]);

> S := unapply(subs(s=sol[1],[Y[1],Y[2]]),t,r):
T := unapply(subs(s=sol[2],[Y[1],Y[2]]),t,r):

>

>

This piece of the picture shows all the points involved

> pl1 :=(t,r) ->plots[pointplot]({X(t,r),rcX(t,r),Q(t),R(t),P(t),S(t,r),T(t,r)},symbol=circle,symbolsize=8,color=red):

This piece shows all the important segments

> pl2 := (t,r)->plot({[X(t,r),rcX(t,r)],[X(t,r),Q(t,r)],[Q(t),R(t),P(t),Q(t)],[S(t,r),X(t,r),T(t,r),S(t,r)],[P(t),rcX(t,r)]},color=[blue,red,magenta]):

This piece labels certain points: P, X and 1/conjugate(X)

> pl3:=(t,r)->plots[textplot]({[op(X(t,r)+[.1,0]),`X`],
[op(rcX(t,r)+[-.8,-.1]),`1/conjugate(X)`],[op(P(t)+[0,.1]),`P`]},align={ABOVE,RIGHT}):

This combines the pieces into a frame.

> frame:= (t,r)->plots[display]([pl1(t,r),pl2(t,r),pl3(t,r),c],scaling=constrained);

So if t = .5 and r = .3

> frame(.5,.3);

In colors, the theorem says that as long as X stays above the vertical blue segment (but on the same line), the slanting red line goes through P.

Here we are animating a sequence of frames.

> plots[display]([
seq(frame(.6 +i/64,1-i/16),i=1..15)],insequence=true,
scaling=constrained,axes=none);

>