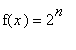On the Structure and Cardinality of the Semigroup of Chebychev Polynomials Mod

by Peng Lou, Dunbar High School, Lexington, Ky

Abstract: In this paper, we will describe the project started a year ago to investigate semigroups of polynomials.

.....

Basic Terminology and Theorems of Semigroup Theory

A binary operation on a set is mapping each ordered pair of a set to an element of the set.

A binary operation * on a set is said to be associative if a*(b*c) = (a*b)*c for all a, b, and c in the set.

A set with an associative binary operation applied on it is called a semigroup.

Put in here the definitions and examples of a semigroup, commutative semigroup, subsemigroup, idempotent element, identity element, zero element, nilpotent element, cyclic semigroup, group, unit, group of units, homomorphism, homomorphic image, isomorphic semigroups.

Include among your examples the semigroup N of non-negative integers under multiplication and the integers mod n .

Also, put in here these theorems and their proofs :

T. A subsemigroup of a semigroup is a semigroup

T. A subsemigroup of a commutative semigroup is commutative.

T. If S is a commutative semigroup, then the nilpotent elements form a subsemigroup.

Several others ...

Semigroups of Polynomials

The Semigroup of Chebychev Polynomials

Definition: The Chebychev polynomials are defined recursively as follows:

Let represent the 0th Chebychev polynomial, the 1st, and the nth, and so on.

= 1 ; = x;

The above mentioned polynomials could also be expressed using an explicit definition, which the paper will go into greater detail in a later juncture.

The set of Chebychev polynomials isalso a semigroup because it is closed under the binary operation of composition. That is to say, when a Chebychev polynomial is composed with another such polynomial, the result remains an element in the set.

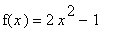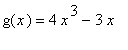Example: Let ( ) and ( ), then ( )

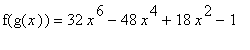It could be further observed that if and , then = .

The associativity of the composition operation on the Chebychev polynomials need not be explicitly proven since if any two elements in the set composed with each other yield another element in the set, the same conclusions could be drawn if a third element is composed with the result of the previous composition.

Include in here a discussion of the original purpose of the Chebychev polynomials

Include also the alternative definition of Cheb in terms of arccos and cos.

Include also your derivation, including the maple code, for your formula for the

coefficients of the nth Chebychev polynomial.

First, let's examine the explicit formula for the Chebychev polynomials. Although such a formula existed before the compilation of this paper, the only known example was one that involved the trigonometric functions arccos and cos .

Formula 1:

Since this project is interested in finding the number of Chebychev polynomials after modding by , the aforesaid formula offers little assistance. Rather, a purely numerical formula needs to be derived in order to have some bearing on solving the problem. By manipulating the recursive definition of the Chebychev polynomials, the following closed form formula is generated.

You need to explain how you derived this using generating functions.

Formula 2:

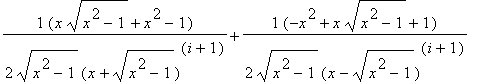
In order to assertain the validity of the above definition, both formulas were plotted on the same axis using Maple as shown below.

> t := proc(i)
if i = 0 then 1 elif i=1 then x else expand(2*x*t(i-1)-t(i-2)) fi end;

> plt := n-> plot({t(n),c(x,n),arccos(n*cos(x))},x=-1..1);

> plt(5);

As illustrated by the graph, the two forumlas are identical.

No. They appear to be identical.

Note: The red plot represents the graph of the first formula. Due to the restrictions on the domain of the function arccos (-1 to 1,) the graph is limited to these values.

As evident from the complexity of the second formula, applying the modding function on it would be extremely time consuming if not futile.

How do you know the Chebychev polynomials form a semigroup?

Since the semigroup of Chebychev polynomials cannot be treated as a whole, perhaps it is possible to divide it into several subsemigroups and count each of them seperately.

Definitions Let S be a semigroup and s be an element of S. s is an idempotent of S if s^2 = s. s is the identity of S if sy=ys=y for all y in S. x is the zero of S if sy=ys=s for all y in S.

After observing the semigroup of Chebychev polynomials, it could be observed that (1) is a zero and ( x ) is an identity under the binary operation of composition. It is also evident that both elements are idempotent. Given the property of the Chebychev polynomials that one element composed with another yields a third, it could be seen that any element in the set, after composing with itself a variable number of times, will eventually yield either a zero element or an identity element.

What you say is not true. You must pass to the chebychev polynomials mod 2^n for this to become true.

Thus, if 1 and x are the only idempotent elements in the semigroup of Chebychev polynomials, then each member of set will power down to one or the other.

Here put a description of Cheb, the semigroup of chebychev polys and its homorphic images Cheb[m], m = 0..infinity

Definition: The set of all elements in the semigroup of Chebychev polynomials that power down to zero element(s) form a subsemigroup called nilpotents.

This is not a definition. It is a theorem which must be proven.

Definition: The set of all elements in the semigroup of Chebychev polynomials that power down to identity element(s) form a subsemigroup called units.

Same comment

Theorem: for all n is either a nilpotent or an unit.

Prove: The only idempotent elements of are 1 and x .

Proof. The proof proceeds by induction on n.

For , the only elements are 1 and x, and these are idempotent.

Assume there are only two idempotent elements in , namely 1 and x , and suppose that is idempotent in .

Then, (definition of idempotency)

and mod 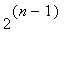equals either 1 or x .

Case 1: Assume = 1 and

+ ...... + ( ) where is a constant

+ ...... +

= [ + ...... + 1][ ]

All the non constant terms cancel out because the resulting coefficients are divisible by .

Since is a constant, it must equal 1 because the only possible constant in the Chebychev is 1.

Case 2: Assume

+ ...... +

If = x (mod 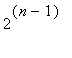) , the constant term can only be multiples of 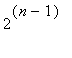, and since the only possible constant terms in are 0, 1, and 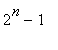, the constant term for in this case is 0.

+ ...... +

But for r from n to 2, = mod = , so = mod = x mod

By mathematical induction, it could be seen that contains only two idempotent elements, 1 and x , for all values of n.

Looking at the polynomials, all the even degree elements have an odd constant term. This is true due to the recursive nature of the Chebychev polynomials. Since all for each contains an odd constant, starting with of 1, all of even degree elements also have odd constants. Thus, after modding by a power of two, these constant terms cannot possibly cancel out, which means that all of even degree are nilpotents, which makes those of odd degree units.

Now there's the matter of determining which part of the cardinality formula of corresponds to that of the units and which part to that of the nilpotents. Using Maple, it could be conjectured that the cardinality of the former is represented by 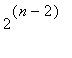and that of the latter by . However, mathematical proof is necessary to confirm such a conjecture.

To accomplish such a task, it may be helpful to be able to calculate any coefficient in , since they're the ones being modded. Using Maple, a matrix of coefficients could be constructed:

The first column represents the numerical designation of the Chebychev polynomial.

After further manipulation, it could be seen that each coefficient could be conveniently expressed as a linear combination of two consecutive powers of two.

When each diagonal of the above matrix is isolated, it could be seen that the coefficients of the linear combinations correspond to subsequent diagonals of the Pascal's triangle. Based on previous knowledge that each element of the Pascal's triangle could be expressed as a combination, the formula for each part of the linear combination that forms each coefficient devised. Now it's a matter of linking each coefficient with the appropriate power of x in the right polynomial. This is done by expressing each coefficient in terms of two variables n and i, n representing the numerical designation of the polynomial, and i is used to distinguish between each term within the polynomial. The formula is as follows:

=

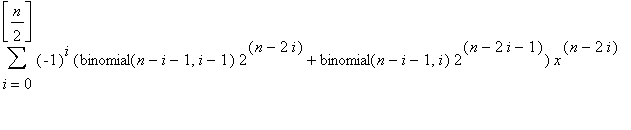
If this formula were true, then it should follow that each should equal to the difference of twice and according to the recursive formula for .

The Semigroup of Chebychev Polynomials mod 2^n

Counting the unit Chebychev Polynomials mod 2^n.

Problem: Count all the unique Chebychev polynomials in the set generated when modded by any power of two

The dyadic part of a number and Lagrange's formula

Note: To mod a polynomial by a number is essentially modding all the coefficients of the polynomial by that integer

Example: 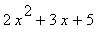mod 2 =

Before venturing into a detailed explication of the project, it is necessary to define several terms and concepts in order to facilitate its understanding.

> ?fermat

>

Unsolved problems

Here you will discuss the problem of determining the structure of and the cardinality of the nilpotent chebychev polynomials mod 2^n. (Unless you solve this problem between now and February 1.)

Bibliography

1. Numerical analysis

2. Theory of Semigroups Clifford and Preston.

An isomorphism between two semigroups S and S' is defined as a one to one function f from S to S' such that for all x, y in S. Semigroups S and S' are said to be isomorphic images of each other.

Example: Let S be the semigroup of additive positive integers and S' be the set of positive powers of 2 together with the operation of multiplication. Then S is said to be isomorphic with S' under the isomorphism