944-14-25 On the classification of double meanders of M-curves of degree 5.
By Anatoly B. Korchagin*, korchag@math.ttu.edu.

A meander of a plane real projective nonsingular curve of degree n is its connected component having n real points of intersection with a line. Only the one-side component of a nonsingular curve of odd degree can be a meander. Let a₁, a₂, ... , a_n and b₁, b₂, ... , b_n be 2n distinct points of intersection of two lines L_a and L_b, respectively, with a component A of a curve of degree n. An orientation of the component A defines a cyclic sequence of these 2n points in A. If, after proper renumbering (if it is necessary), the cyclic sequence is a₁, a₂, ... , a_n, b₁, b₂, ... , b_n then the component A is called a double meander with respect to the lines L_a and L_b. We consider the isotopy classification of unions of two lines and an M-curve of degree 5 having a double meander with respect to the two lines.

944-13-140 On systems of binomials in toric varieties.
By Shalom Eliahou and Rafael H Villarreal*, vila@esfm.ipn.mx.

Let k be any field and 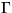the toric set in the affine space A_kⁿ given parametrically by x_i=t₁^d_1i ... t_m^d_mi, 1 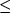i 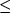n, where D = (d_ij) is an m x n matrix with non-zero columns and whose entries d_ij are non negative integers. Given a set of binomials g₁, ...,g_r in the toric ideal P of k[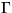], we give a criterion to decide when rad(g₁, ...,g_r) = P and show that this criterion is effective for m=1. This extends to arbitrary dimension, and to arbitrary fields, an earlier result which held only for monomial curves over an algebraically closed field of characteristic zero.

944-13-151 On residually S₂ ideals.
By Claudia Polini* and Alberto Corso, polini@math.hope.

This talk is about cancellation theorems for special ideals in a local Gorenstein ring R. In its simplest form any such theorem says that if I, J and L are R-ideals such that LI 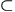JI then L 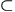J. Using the so called determinant trick, in general one can only conclude that L 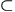JI : I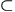 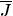, where 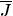denotes the integral closure of J.
To say that cancellation holds for every such ideal L is equivalent to say that the R/J-module I/JI is faithful, that is to say JI : I = J. More generally, one can ask for which positive integers t the equality JI^t : I^t = J holds.
This kind of question is particularly interesting when the ideal J is a reduction of the ideal I, that is I^r+1 = JI^r for some positive integer r. Hence I 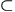JI^r : I^r. Thus, conditions of the kind JI^t : I^t = J, with J a reduction of I, give a severe bound on the reduction number of ideals which admit proper reductions.
Our main result, which estends work of C. Huneke, answers the above questions in the case of ideals satisfying local bounds on the minimal number of generators and some other residual properties.

944-13-159 Depth for complexes, and intersection theorems.
By Srikanth Iyengar*, iyengar@math.missouri.edu.

A new notion of depth for complexes is introduced; this agrees with the classical definition for modules and coincides with earlier extensions to complexes, whenever they are defined. Two "Auslander-Buchsbaum" type theorems are established and using these we give a quick proof of an extension of the Improved New Intersection Theorem (this uses Hochster's big Cohen-Macaulay modules), and also a generalization of the "depth formula" for tensor products of modules.

944-13-180 Noether normalizations of some subrings of graphs.
By Adriàn Alcàntar*, adrian@esfm.ipn.mx.

Let G be a graph on the vertex set V={x₁, ..., x_n} and R=k[x₁, ...,x_n] a polynomial ring over a field k. The monomial subring or edge subring of Gis the k-subalgebra k[G] 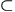R generated by the set of monomials x_ix_j such that x_i is adjacent to x_j. In this report we study (standard) Noether normalizations of k[G]. If G is the complete graph on n vertices we present two explicit Noether are normalizations of k[G], it will turn out that those normalizations can serve as a model to find Noether normalizations of k[G] for some specific graphs.

944-16-201 Serre's Multiplicity Conjectures for Connected Algebras.
By Izuru Mori*, mori@math.uta.edu.

Let $R$ be a noetherian regular local commutative ring and $M,N$ be finitely generated $R$-modules. If $\ell (M\otimes _RN)<\infty$, then Serre defined the intersection multiplicity of $M$ and $N$ by $$\chi (M,N):=\sum _{i=0}^{\infty}(-1)^i\text{length}\Tor ^R_i(M,N).$$ Serre's multiplicity conjectures are: \bigskip {\bf Conjecture} (Serre, 1961) Suppose $\el (M\otimes _RN)<\infty$. Then \begin{itemize} \item{} (Dimension) $\Kdim M+\Kdim N\leq \Kdim R$. \item{} (Vanishing) If $\Kdim M+\Kdim N< \Kdim R$, then $\chi (M,N)=0$. \item{} (Positivity) If $\Kdim M+\Kdim N=\Kdim R$, then $\chi (M,N)>0$. \end{itemize} In this talk, we will prove Serre's multiplicity conjectures for (1) connected algebras (not necessarily commutative) and (2) quantum projective spaces (which are noncommutative analogues of the commutative projective spaces), using the intersection multiplicity defined by $\Ext$ groups instead of $\Tor$ groups. Since these two definitions of intersection multiplicity agree for commutative conneted algebras, the first result is a noncommutative generalization of the result of Peskine and Szpiro. The second result is a generalization of B\'ezout's Theorem.

944-13-206 Generalized Auslander Regular Algebras.
By Roberto Martìnez-Villa*, mvilla@matem.unam.mx.

944-13-248 Noetherian domains inside a homomorphic image of a completion II.
By Heinzer William, Christel Rotthaus* and Sylvia Wiega rotthaus@math.msu.edu.

944-13-259 Associated graded rings of normal ideals.
By Sam Huckaba and Thomas Marley*, tmarley@mathstat.unl.edu.

We show how to use a result of Itoh concerning the vanishing in certain degrees of the local cohomology modules of the Rees algebra of a normal ideal to prove a generalization of the Grauert-Riemenschneider Vanishing Theorem for two-dimensional Cohen-Macaulay varieties. Namely, we prove that if (R, m) is a two-dimensional Cohen-Macaulay local domain and I is an ideal of R such that Proj R[It] is normal, then gr(Iⁿ, R) is Cohen-Macaulay for large n. This follows from a more general result which we will discuss concerning the depths of gr(Iⁿ, R) for large n and I a normal ideal.

944-13-280 Noetherian domains inside a homomorphic image of a completion I.
By William Heinzer, Christel Rotthaus and Sylvia M Wiegand*, swiegand@math.unl.edu.

Over the past sixty years, important examples of Noetherian domains have been constructed from more standard Noetherian domains using power series, homomorphic images and intersections. In this talk, we analyse intersections of form A:=L 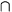(R^* /I), where R is a Noetherian integral domain, L is its fraction field, R^* ("power series in x") is the completion of R with respect to a nonzero nonunit x of R, and I is an ideal of R^* with the property that P 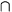R = (0) for each P in Ass(R^*/I). It is not usually true that this procedure yields a Noetherian ring, nor is it usually easy to identify and understand the resulting ring (even if R is the ring of polynomials in two variables over a field). We show that A is Noetherian and computable (from R) provided that the embedding R 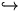(R^*/I)_x is flat.
In Christel Rotthaus' talk, "Noetherian domains inside a homomorphic image of a completion II", she will apply these results to construct specific examples of Noetherian local domains.

944-13-292 Refinements of a Conjecture of Nagata.
By Brian Harbourne*, bharbour@math.unl.edu.

944-13-302 Integral closure, conductors and direct summands.
By Daniel Katz*, dlk@math.ukans.edu.

Let S be a normal Noetherian domain, w a root of a monic irreducible polynomial over S and R the integral closure of S[w]. Let J denote the conductor of R into S[w]. We discuss the relationship between the following conditions:
(a) J is not contained in MS[w] for all maximal ideals M of S and
(b) S is a direct summand of R.

944-13-304 Depth of symmetric algebras of certain ideals.
By Mark R Johnson*, mark@math.uark.edu.

A well-known result of Herzog, Simis and Vasconcelos guarantees the Cohen-Macaulayness of the symmetric algebra for an ideal which satisfies sliding depth and the Fitting condition F₀. Without the assumption of sliding depth, we use some recent results on the Cohen-Macaulayness of the blow-up ring to compute in some cases the depth of the symmetric algebra.

944-13-307 Divisors of a Rees algebra.
By Susan E Morey* and Wolmer V Vasconcelos, sm26@swt.edu.

Suppose R is a Noetherian ring which has a canonical module and I is an ideal of R. The divisors of a Rees algebra R[It] are the rank one R[It]-modules which satisfy Serre's condition S₂. Two divisors of particular importance are the canonical module of R[It] and the fundamental divisor Ext^n-1_B(IR[It], w_B) where B=R[T₁, ... , T_n] when I is generated by n elements. We will discuss properties of the divisors and how they relate to properties of R[It]. In particular we are interested in discovering when the Rees algebra is Cohen-Macaulay.

944-13-311 Associated primes of toric initial ideals.
By Rekha R Thomas* and Serkan Hosten, rekha@math.tamu.edu.

It is an open question to characterize those monomial ideals that occur as initial ideals of toric ideals. In this talk I will present some recently found special properties that are satisfied by the associated primes of toric initial ideals.

944-13-313 Fat point ideals for 8 or fewer points of P².
By Brian Harbourne, Sandeep Holay and Stephanie Fitchett*, sfitchet@math.duke.edu.

944-13-314 Strange summands of direct sums of copies of a module.
By Roger A Wiegand*, rwiegand@math.unl.edu.

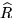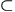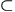Let (R, m) be a local ring with m-adic completion . For a finitely generated R-module M, let S_n be the set of isomorphism classes of indecomposable direct summands of the direct sum of n copies of M. Even when M is indecomposable, the sets S_n can grow large as n increases. (However, each S_n is finite, and the sequence S₁ S₂ S₃ 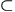... 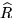eventually stabilizes.) We will discuss the appearance of these new indecomposable summands vis à vis splitting in the completion and the subtle question of which -modules are extended from R-modules.

944-13-330 On the torsion freeness of symmetric powers of ideals.
By Alexandre Tchernev*, tchernev@math.missouri.edu.

944-13-341 On low rank algebraic vector bundles.
By N. Mohan Kumar, Chris Peterson* and A. Prabhakar Rao, peterson@math.wustl.edu.

944-13-364 Normalization of toric varieties.
By Joseph Brennan*, brennan@hazlett.math.ndsu.NoDak.edu.

The construction of the normalization of a monomial subring of a polynomial ring will be given. Special attention will be given to the case of subrings associated to graphs in the sense of Simis-Vasconcelos-Villarreal (see J. Algebra 199 (1998) 281-289).

944-13-368 Gorenstein Modules.
By Graham J. Leuschke*, gleuschk@math.unl.edu.

A Gorenstein module for a Cohen-Macaulay ring R is a maximal Cohen-Macaulay module G of finite injective dimension. The concept is a generalization of the canonical module, and Gorenstein modules enjoy several similar properties. We will discuss existence and properties of Gorenstein modules and applications to the representation theory of local rings.

944-13-378 On The Gauss-Manin Connection.
By Herbert Kanarek*, herbert@math.unam.mx.

944-13-382 Some results on rational surfaces and Fano varieties.
By Francisco J Gallego and Bangere P Purnaprajna*, purna@math.ukans.edu.