




Next: Incidence Geometry
Up: Neutral and Non-Euclidean Geometries
Previous: Proof Creativity
We will accept the Rules of Reasoning that we have been discussing as
our logic rules in our mathematical system. There are several ways in
which we can go about setting forth our axioms and undefined terms for
geometry. We can keep the number of axioms down to a very few, in which case
we need a large number of undefined terms, relations, and operations. We can
keep the number of undefined terms, relations, and operations to a small
number, thus requiring a larger number of axioms. We will actually work with
the Axiom system set up by David Hilbert in 1899 in his book Foundations
of Geometry. He not only clarified Euclid's definitions but also filled in
the gaps in some of Euclid's proofs. Hilbert recognized that Euclid's proof
for the side-angle-side criterion of congruence in triangles was based on an
unstated assumption (the principle of superposition) and that this criterion
had to be treated as an axiom. He built on the earlier work of Moritz Pasch,
who in 1882 published the first rigorous treatise on geometry; Pasch made
explicit Euclid's unstated assumptions about betweenness. At the same time we
could have used the axioms set forth by Garret Birkhoff. These axioms are the
ones with which you are more familiar, being the basis for the texts in High
School Geometry. I have included both sets of axioms, so that you can compare
the two. We will work exclusively with the Hilbert axioms. An interesting
exercise is to prove everything that we will
prove using Birkhoff's axioms. Some proofs are easier, and some are harder.
First, let us set our undefined terms. They will be
- point,
- line,
- incidence, (a point being incident with a line)
- betweenness,
- congruence.
These objects are to be taken as undefined terms. We will not attempt to make
a definition of any of them. However, when we wish to look at a specific
example of our geometry, called a model, we will have to establish how
each of these undefined terms is to be interpreted. For example, if we wish to
look at the model where points are ordered pairs coming from the usual
Cartesian plane and lines are the usual straight lines in the Cartesian plane,
then we would be able to easily state what it means for a point to be incident
with a particular line, what it means for one point to lie between two other
points and what it means for two line segments to be congruent. We could
change our example though to be a set of seven points, where lines would be
ordered pairs of points, incidence would be set inclusion and betweenness and
congruence would be meaningless. The particular model that we choose will
determine our interpretation of the terms, but will not define them.
At this point we need to make some definitions. In order to do this we need
our axiom system. I shall include all of the axioms here, though we will
discuss them in more detail later.
Hilbert's Axioms for Neutral Geometry
- I-1:
- For every point P and for every point Q not equal to P
there exists a unique line
 that passes through P and Q.
that passes through P and Q.
- I-2:
- For every line
 there exist at least two distinct
points incident with
there exist at least two distinct
points incident with  .
.
- I-3:
- There exist three distinct points with the property that no
line is incident with all three of them.
GROUP II: BETWEENESS AXIOMS
- B-1:
- If
 , then A, B, and C are three distinct
points all lying on the same line, and
, then A, B, and C are three distinct
points all lying on the same line, and 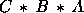 .
.
- B-2:
- Given any two distinct points B and D, there exist points
A, C, and E lying on
 such that
such that
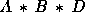 ,
,  , and
, and 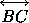 .
.
- B-3:
- If A, B, and C are three distinct points lying on the
same line, then one and only one of the points is between the other two.
- B-4:
- (PLANE SEPARATION AXIOM) For every line
 and
for any three points A, B, and C not lying on
and
for any three points A, B, and C not lying on  :
:
- (i)
- if A and B are on the same side of
 and B and
C are on the same side of
and B and
C are on the same side of  , then A and C are on the same side of
, then A and C are on the same side of
 .
.
- (ii)
- if A and B are on opposite sides of
 and B
and C are on opposite sides of
and B
and C are on opposite sides of  , then A and C are on the same
side of
, then A and C are on the same
side of  .
.
GROUP III: CONGRUENCE AXIOMS
- C-1:
- If A and B are distinct points and if A' is any
point, then for each ray r emanating from A' there is a
unique point B' on r such that
 and
and 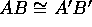 .
.
- C-2:
- If
 and
and 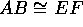 , then
, then  .
Moreover, every segment is congruent to itself.
.
Moreover, every segment is congruent to itself.
- C-3:
- If
 , A'*B'*C',
, A'*B'*C',
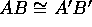 , and
, and 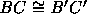 , then
, then  .
.
- C-4:
- Given any
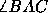 and given any ray
and given any ray  emanating
from a point A', then there is a unique ray
emanating
from a point A', then there is a unique ray 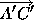 on a given
side of line
on a given
side of line  such that
such that  .
.
- C-5:
- If
 and
and  ,
then
,
then  . Moreover, every angle is congruent to itself.
. Moreover, every angle is congruent to itself.
- C-6:
- (SAS) If two sides and the included angle of one
triangle are congruent respectively to two sides and the included angle of
another triangle, then the two triangles are congruent.
GROUP IV: CONTINUITY AXIOMS
- ARCHIMEDES' AXIOM:
- If AB and CD are any segments, then
there is a number n such that if segment CD is laid off n times on the ray
 emanating from A, then a point E is reached where
emanating from A, then a point E is reached where
 .
.
- DEDEKIND'S AXIOM:
- Suppose that the set of all points on a
line
 is the union
is the union  of two nonempty subsets
such that no point of
of two nonempty subsets
such that no point of 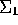 is between two points of
is between two points of  and
vice versa. Then there is a unique point, O, lying on
and
vice versa. Then there is a unique point, O, lying on  such that
such that
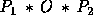 if and only if
if and only if  .
.
(The following two Principles follow from Dedekind's Axiom, yet are at times
more useful.)
- CIRCULAR CONTINUITY PRINCIPLE:
- If a circle
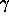 has one
point inside and one point outside another circle
has one
point inside and one point outside another circle 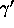 , then the two
circles intersect in two points.
, then the two
circles intersect in two points.
- ELEMENTARY CONTINUITY PRINCIPLE:
- If one endpoint of a
segment is inside a circle and the other outside the circle, then the segment
intersects the circle.
Birkhoff's Axioms for Neutral Geometry
 .
.
- AXIOM 1:
- There exist nonempty subsets of
 called
lines, with the property that each two points belong to exactly
one line.
called
lines, with the property that each two points belong to exactly
one line.
- AXIOM 2:
- Corresponding to any two points
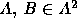 there
exists a unique number
there
exists a unique number  , the
distance from A to B, which is 0 if and only if A = B.
, the
distance from A to B, which is 0 if and only if A = B.
- AXIOM 3:
- (Birkhoff Ruler Axiom) If k is a line and
R denotes the set of real numbers, there exists a one-to-one
correspondence (
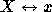 ) between the points
) between the points  and the
numbers
and the
numbers 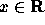 such that
such that

where 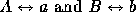 .
.
- AXIOM 4:
- For each line k there are exactly two nonempty
convex sets
 satisfying
satisfying
- i)
-
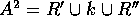
- ii)
-
 . That is, they are pairwise disjoint.
. That is, they are pairwise disjoint.
- iii)
- If
 then
then  .
.
- AXIOM 5:
- To each angle
 there exists a unique real
number x with
there exists a unique real
number x with  which is the (degree) measure of the
angle
which is the (degree) measure of the
angle

- AXIOM 6:
- If
 , then
, then

- AXIOM 7:
- If
 is a ray in the edge, k, of
an open half plane H(k;P) then there exist a one-to-one correspondence
between the open rays in H(k;P) emanating from A and the set of real
numbers between 0 and 180 so that if
is a ray in the edge, k, of
an open half plane H(k;P) then there exist a one-to-one correspondence
between the open rays in H(k;P) emanating from A and the set of real
numbers between 0 and 180 so that if 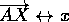 then
then

- AXIOM 8:
- (SAS) If a correspondence of two triangles, or a
triangle with itself, is such that two sides and the angle between them are
respectively congruent to the corresponding two sides and the angle between
them, the correspondence is a congruence of triangles.
Definition: The plane is the collection of all points and
lines.
Definition: The segment
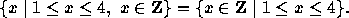
A and B are the endpoints of the
segment AB.
Definition: Given points O and A in the plane. The set of points P such
that  is a circle with center O. Each segment OP
is called a radius .
is a circle with center O. Each segment OP
is called a radius .
Definition: The ray
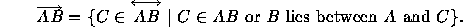
 emanates from A and is
part of
emanates from A and is
part of  .
.
Definition: The rays  and
and 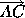 are opposite if they are
distinct, emanate from A, and are part of the same line
are opposite if they are
distinct, emanate from A, and are part of the same line
 .
.
Definition: An angle with vertex A is
a point A together with
2 non-opposite rays  and
and 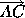 , called the sides ,
emanating from A. Denote this angle by
, called the sides ,
emanating from A. Denote this angle by 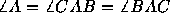 .
.
Definition: If  and
and 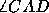 have a common side
have a common side  and the other two sides
and the other two sides  and
and 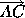 form opposite rays, the
angles are supplements or supplementary angles .
form opposite rays, the
angles are supplements or supplementary angles .
Definition: An angle  is a right angle
if it has a supplementary angle to which it is congruent.
is a right angle
if it has a supplementary angle to which it is congruent.
Definition: Two lines  and m are parallel
if they do not intersect; i.e., if no point lies on both of them. Denote this by
and m are parallel
if they do not intersect; i.e., if no point lies on both of them. Denote this by
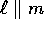 .
.
Definition: Two lines  and m are perpendicular
,
and m are perpendicular
,  ,
if they have a point A in common and there exist rays
,
if they have a point A in common and there exist rays  , a part of
, a part of
 , and
, and 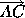 , a part of m, such that
, a part of m, such that 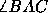 is a right
angle.
is a right
angle.





Next: Incidence Geometry
Up: Neutral and Non-Euclidean Geometries
Previous: Proof Creativity
david.royster@uky.edu
![]()
![]() is a circle with center O. Each segment OP
is called a radius .
is a circle with center O. Each segment OP
is called a radius .
![]()
![]() emanates from A and is
part of
emanates from A and is
part of ![]() .
.
![]() and
and ![]() are opposite if they are
distinct, emanate from A, and are part of the same line
are opposite if they are
distinct, emanate from A, and are part of the same line
![]() .
.
![]() and
and ![]() , called the sides ,
emanating from A. Denote this angle by
, called the sides ,
emanating from A. Denote this angle by ![]() .
.
![]() and
and ![]() have a common side
have a common side ![]() and the other two sides
and the other two sides ![]() and
and ![]() form opposite rays, the
angles are supplements or supplementary angles .
form opposite rays, the
angles are supplements or supplementary angles .
![]() is a right angle
if it has a supplementary angle to which it is congruent.
is a right angle
if it has a supplementary angle to which it is congruent.
![]() and m are parallel
if they do not intersect; i.e., if no point lies on both of them. Denote this by
and m are parallel
if they do not intersect; i.e., if no point lies on both of them. Denote this by
![]() .
.
![]() and m are perpendicular
,
and m are perpendicular
, ![]() ,
if they have a point A in common and there exist rays
,
if they have a point A in common and there exist rays ![]() , a part of
, a part of
![]() , and
, and ![]() , a part of m, such that
, a part of m, such that ![]() is a right
angle.
is a right
angle.