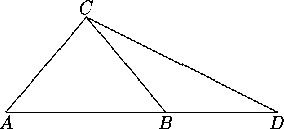
Figure 11.1: Triangle inequality
We will now take up the Axioms of Continuity. First, we will prove the two Continuity Principles and then discuss some of the different uses of the Continuity Axioms in our work.
First, we shall need the famous Triangle Inequality. It is usually proved after we have given a measure to line segments, but that is not necessary.
Proposition 10.1:[Triangle Inequality] If A, B, and C are three noncollinear points, then AC<AB+BC, where the sum is segment addition.

Figure 11.1: Triangle inequality
Proof: There is a unique point D such that ![]() and
and
![]() by the first congruence axiom. Then
by the first congruence axiom. Then ![]() by Proposition 8.1. Now,
by Proposition 8.1. Now, ![]() and since
and since ![]() we
have that
we
have that ![]() . By Proposition 7.7
. By Proposition 7.7 ![]() is between
the rays
is between
the rays ![]() and
and ![]() . Then, by definition,
. Then, by definition, ![]() . By Proposition 8.12 and what we have just shown,
. By Proposition 8.12 and what we have just shown, ![]() . Thus, by Proposition 10.5 AD>AC, and we are done.
. Thus, by Proposition 10.5 AD>AC, and we are done.
Theorem 10.1:[Elementary Continuity Principle] If one endpoint of a segment is inside a circle and the other outside, then the segment intersects the circle.
Proof: Let ![]() be a circle centered at O with radius OR, so
that
be a circle centered at O with radius OR, so
that ![]() . Let AB be the above segment. Let
. Let AB be the above segment. Let
![]() and
and
![]() . Let
. Let
![]()
Note that neither of ![]() or
or ![]() is empty. We wish to show that
these two sets form a Dedekind cut of the segment AB. There are then several
things to show.
is empty. We wish to show that
these two sets form a Dedekind cut of the segment AB. There are then several
things to show.
Now, assume that ![]() . Then, for the first case, assume that
OA<OX. Hence,
. Then, for the first case, assume that
OA<OX. Hence, ![]() . Again,
. Again, ![]() which
implies OC<OX<OR. Thus,
which
implies OC<OX<OR. Thus, ![]() . If OA>OX reverse the labels in the
previous argument and we again find that
. If OA>OX reverse the labels in the
previous argument and we again find that ![]() .
.
Thus, ![]() and
and ![]() form a Dedekind cut of AB. Let M be the
cut point.
form a Dedekind cut of AB. Let M be the
cut point.
CLAIM: ![]() .
.
Assume OM<OR. This puts ![]() and so
and so ![]() . Now, there is a
segment which is less than the difference between OM and OR. Let M' be a
point outside
. Now, there is a
segment which is less than the difference between OM and OR. Let M' be a
point outside ![]() and on AB so that MM' is congruent to that segment.
Thus, we have that
and on AB so that MM' is congruent to that segment.
Thus, we have that ![]() . By the Triangle Inequality we have that
. By the Triangle Inequality we have that
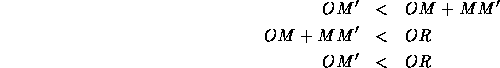
But, ![]() so that
so that ![]() : a contradiction.
: a contradiction.
Assuming that OM>OR we use the same technique to arrive at a contradiction.
Thus, ![]() and
and ![]() .
.