A line 
subdivides an angle if it passes through the vertex of
the angle and intersects the interior of the angle.
Let P be an arbitrary point in the hyperbolic plane. The pencil of
lines through P, denoted 
is the set of all lines coincident
with P.
Theorem 13.1: If 
then there exists an angle with vertex at P
whose interior contains and whose bisector is perpendicular to .
Proof: In the pencil let p be the perpendicular to
and let 
be perpendicular to p at P. Thus, we know
that 
. By the Universal Hyperbolic Theorem there is
another line 
which does not intersect . Since n is
distinct from m, n is not perpendicular to p. Thus, one pair of the
vertical angles formed by p and n is a pair of acute angles. Thus, there
exists a ray 
so that
where Q is the foot of P in .
Now, by Congruence Axiom 4 there is a ray 
on the opposite
side of p from A so that 
. The line
does not intersect . If it did, then let R be the point
of intersection. Choose R' on the same side of p as A so that 
. Then by SAS 
. Thus, 
. Thus, by Congruence Axiom 4 
. This implies that 
, which is a contradiction.
Therefore, 
.
Clearly, 
bisects 
. We only need to show that is
contained in the interior of , or that every point on lies
in the interior of .
Let 
be on the same side of p as A, and let Y be the unique
point on on the opposite side of p as X so that 
. Now,
we know that the ray lies in the interior of 
and, in
fact, using an abuse of notation, 
.
Claim: 
lies in the interior of 
. Likewise,
lies in the interior of 
.
To prove this claim, first note that since X is on the same side of
as A, every point of lies on the same side of
p as A. Thus, we are left only to show that if 
then R is
on the same side of 
as Q. This must be the case, for if not
we would have that , a contradiction. Thus, the above
claim is true.
We then have that 
which from above
must lie in the interior of .
Corollary: Every line in that intersects subdivides
the angle .
We have almost proven the following result.
Theorem 13.2: If then there is a unique angle with the
following properties:
in its interior;
;
.
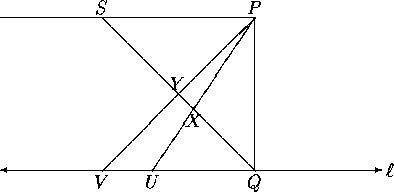
Proof: To prove that this angle exists, we need to construct the sides
of the angle. We already know that there are angles with vertex at P that
contain the line . We want to prove much more in this theorem. In some
sense we are proving that there is a smallest such angle.
Let S be a point on the line m which is the perpendicular at P to the
perpendicular through P to . Consider the line 
. Let
be the set of all points T on SQ, such that 
intersects , together with all points on the ray opposite to 
.
Let 
. By the Crossbar Theorem if
and 
, then the entire subsegment 
.
Hence, 
is a Dedekind cut. By Dedekind's Axiom there is a
unique point X on such that for 
,
if and only if 
and 
,
and 
.
By the definition of and 
rays below 
all
intersect and rays above do not. Now, we wish to prove that
Assume on the contrary that 
. Choose a point V on
so that 
. Since V and U are on the same side of
(Exercise 9, Chapter 3), V and P are on opposite sides, so
that VP meets SQ in a point Y. By Proposition 7.7 we have that
. Thus, 
. This is impossible, for if
, then 
. Thus, does not
meet .
Doing the same construction on the opposite side of 
at
P gives us a similar ray 
with similar properties. We need to
show that 
. Assume not, then we may assume that
. By Congruence Axiom 4 there is a ray 
between and such that 
. By
the properties of , must intersect . Let R be
the point on on the opposite of from R' so that
. Then by SAS 
. This
implies that 
. By Congruence Axiom
4 we have to have that 
or 
, a
contradiction. Thus, .
Checking the properties, clearly bisects the angle, the angle
contains and by the definition of the ray any line that
subdivides the angle intersects .
For this angle at P is called the fan
angle of P and
, and will be denoted by 
.