Return to the Klein Model

Now, we have that the Poincaré model is a model for hyperbolic geometry. Since the Klein model is isomorphic to the Poincaré model, it too is a model of the hyperbolic plane, but that does not explain why we do the things the way that we do.

We shall use another isomorphism to study the Klein model. Let denote the unit sphere in Euclidean three-space,

and let denote the equatorial circle

We shall consider the interior of for both the Klein and Poincaré models. Let N=(0,0,1) and map the interior of onto the southern hemisphere by projection from N.

 
Figure 17.14: Central Projection from N

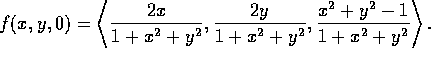
Now, apply the projection up to the xy-plane,

The composition of these two maps is the map from the interior of to itself given by:

A common way of studying the circle is to recall that the Euclidean plane can represent the complex line by the point (a,b) represents the complex number a+bi. The circle is then the set . Defining the modulus of z by , we can rewrite the above function F by

Clearly, F maps a diameter of onto itself, but fixes only the origin and the endpoints of the diameter. In fact, as F maps the interior of onto itself, it fixes only the origin and the points on .

Consider a p-line in , say --a circle orthogonal to . . What is ?

Claim: If and PQ is the chord of in , then .

Proof: Let C=(a,b) be the center of . Then we found P and Q by taking the circle with CO as diameter and intersecting it with . It s center is and its radius is . Applying standard analytic geometry we find that its equation is . Intersecting this with gives

for the line joining P and Q.

Now CQ is perpendicular to OQ since and are orthogonal circles. Thus, or where r is the radius of . Then has equation

Let . Put F(A)=(u,v). Solving we find and . Thus, au+bv=1 which implies that .

We can now justify the definitions we made earlier in the Klein model.

• if and only if .
• if and only if .

PERPENDICULARITY: Now, we see that if and only if in the Poincaré model.

1. If and m are both diameters, then and are both diameters. In fact, and . Hence, the usual Euclidean meaning applies.
2. Assume that only is a diameter. Then . is a circular arc perpendicular to . Thus, the tangent to is perpendicular to and passes through the center of . m is the chord of . Since passes through this center, is the perpendicular bisector of m in the Euclidean sense. Therefore, is perpendicular to m in our previous definition. Conversely, if , then is the perpendicular bisector of m. Thus, passes through the center of the circle and is perpendicular to the circular arc .
3. Assume that neither nor m is a diameter. and are arcs of circles and orthogonal to .
   1. Suppose in the Poincaré model. By one of the facts, the center of is and that of is P(m). We need to show that m passes through , then we will have that .

      Let . Since and are orthogonal inversion in interchanges P and Q, since and are also orthogonal. Thus, P=Q' in and the Euclidean line through P and Q--namely m--passes through the center of , which is .

   2. Suppose m passes through . Then P=Q' in so that and are orthogonal.