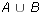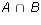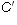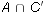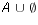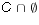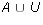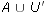
|
College Algebra |
Chapter 1: Sets (Exercises)
1.1 Sets, elements, and subsets
- Review the vocabulary: set, element of a set, empty set, proper subset, subset, equality of sets, universal set.
- List out the elements of each of the following sets. Use curly brackets
notation to specify the set:
- The set of positive integers greater than 6 and less than 12.
- The set of positive odd integers less than 15.
- The set of positive integers less than 50 which are multiples of both 3 and 4.
- The set of non-negative rational numbers less than 1 which can be expressed as a fraction with numerator and denominator positive integers no larger than 4.
- Describe in set notation not using a list each of the following sets.
- A = {2, 4, 6, 8, 10}
- B = {6, 12, 18, 24, 30, 36}
- C = {1, 3/5, 3/7, 1/3, 3/11, 1/4}
- D = {January, March, May, July, August, October, December}
- Let S = {A, E, I, O, U} and T = {O, U}. Mark each of the following
True or False:
-
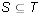
-
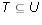
- T has exactly two proper subsets.
- S has exactly five proper subsets.
- T is a proper subset of S.
- T has exactly four subsets.
- The set {A, E, I} has exactly eight subsets.
- The set S has exactly
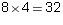 subsets.
subsets.
-
- How many subsets does a set of n elements have?
- Which of the following sets are equal? A = {a, b, c}, B = {c, b, a}, and C = {a, b, c, c, b, a}.
1.2 Operations on Sets
- Review the following vocabulary: intersection, union, complement, disjoint sets, ordered and unordered pair, cartesian product, first and second coordinate of an ordered pair.
- Explain why one doesn't refer to the first coordinate of an unordered pair.
- Let U = {1,2,3,4,5,6,7,8,9} be the universe with sets A = {1,2,3,4},
B = {2,4,6,8}, and C = {6,7,8,9}. List out the elements of each of the
following sets.
-
- Let U = {a, b, c, d, e, f, g, h} be the universe. Let A = {a,b,c,d},
B = {b,d,e,f}, and C = {c,d,f,g}. Calculate each of the following pairs
of sets. Are each of the sets in each pair equal?
-
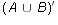 and
and 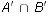
-
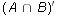 and
and 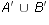
-
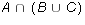 and
and 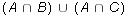 .
.
-
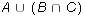 and
and 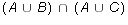 .
.
-
- Use Venn diagrams to illustrate why it is reasonable to think
that the results of last exercise are true generally. Do the same
for each of the following:
-
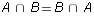
-
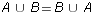
-
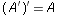
-
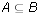 if and only if
if and only if 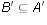
-
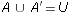
-
- Explain why the union operation is commutative.
- Explain why the intersection operation is associative.
- Explain why intersection distributes over union.
- Explain why one of De Morgan's rules is true.
1.3 A Mathematical Anomaly
- You have seen how working with sets whose elements are arbitrary
can lead to logical contradictions. It remains to see how the concept of
a universal set resolves Russell's paradox. Fix a universal set U. Now
the set of sets which are not self containing must take its elements from U.
So, we are dealing with the set
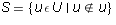
- Show that if
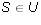 , then Russell's paradox is alive and
well, i.e. you still have a contradiction.
, then Russell's paradox is alive and
well, i.e. you still have a contradiction.
- Why is the paradox resolved?
- Show that if
1.4 Relations and Functions
- Review the vocabulary: relation, function, domain, range, graph, independent and dependent variables, injective, surjective, bijective, one-to-one correspondence, equal cardinality, cardinality n, finite and infinite sets, function of two variables, operator.
- Find the domain and range of each of the following functions:
-
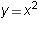
-
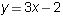
-
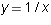
-
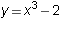
- The function which calculates the birth mother of a first born child.
-
- Let U = {1,2,3,4,5,6,7,8,9} be the universe, A = {1,2,3,4,5,6}
and B = {5,6,7,8,9}. Letting n(S) denote the cardinality of the
finite set S, calculate the following:
-
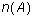 and
and 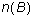
-
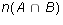
-
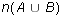
-
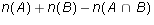
-
- Based on the results of the last exercise, make a conjecture about
how to calculate
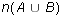 . Use a Venn diagram to
test the plausibility of your conjecture.
. Use a Venn diagram to
test the plausibility of your conjecture.
- Try to prove your conjecture.
- All 1200 of the students were required to take either the SAT or ACT exam. Records show that 800 took the ACT and 750 took the SAT. How many students took both?
All contents © copyright 2002 K. K. Kubota. All rights reserved