Examples of implicit differentiation and plotting with Maple

> g:= x^4+y^4=16;

Here is how to compute the first derivative of y with respect to x:

> implicitdiff(g,y,x);

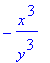
Here is how to take two derivatives of y with respect to x:

> implicitdiff(g,y,x,x);

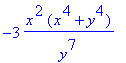
To plot implicitly:

> with(plots):

> implicitplot(g,x=-2..2,y=-2..2,scaling=constrained);

Let's figure out a tangent line when x=1.

> solve(1+y^4=16,y);

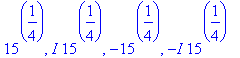
There are two real solutions. Let's use y=15^(1/4) for our example. Then the point on the curve is (1,15^(1/4)). To find the slope of the tangent line, we substitute these values into the expression for the derivative -x^3/y^3:

> a:=1; b:=15^(1/4); m:=-a^3/b^3;

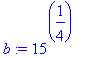
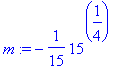
Use the point-slope formula to get the equation of the tangent line:

> line:= (y-15^(1/4))=m*(x-1);

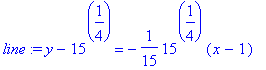
> implicitplot({g,line},x=-2..4,y=-2..4,scaling=constrained);

Here is an example of orthogonal families. First we plot the first family in blue:

> G1:=implicitplot({seq(x*y=c,c=-10..-1),seq(x*y=c,c=1..10)}, x=-5..5,y=-5..5, scaling=constrained, color=blue): display(G1);

Then we plot the second family in red:

> G2:=implicitplot({seq(x^2-y^2=c,c=-10..-1),seq(x^2-y^2=c,c=1..10)}, x=-5..5,y=-5..5, scaling=constrained, color=red): display(G2);

Now we plot them together:

> display({G1,G2});

>