


Next: About this document
Exam #3 Information
The exam will be Wednesday, November 18, 5-7 pm, in Memorial Hall.
Questions will be drawn from Sections 3.4 and 4.1-4.5. Calculators
are permitted, but you will still have to show your work.
BE SURE YOU CAN DO ALL THE HOMEWORK PROBLEMS QUICKLY AND CONFIDENTLY
WITHOUT LOOKING AT YOUR NOTES OR AT THE BOOK.
Some basic information (but NOT a substitute for reading the book and
reworking the homework problems):
- Practical Optimization Problems.
- Find a function of a single variable to
maximize or minimize. You may have a function of two variables and
need to use some other equation to eliminate of the variables from
your function.
- Pay attention to the domain of your function.
- After you have found the first order critical numbers, remember to
check using the first or second derivative tests whether you have
a maximum or minimum at the various points. Don't forget to check the
endpoints of your domain if you have any.
- Exponential Functions.
-
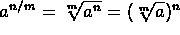 .
. -
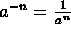 .
. -
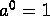 if
if 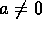 .
. -
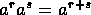 .
. -
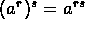 .
. -
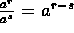 .
. - Know what the graph of
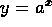 looks like when a>1 and when
a<1.
looks like when a>1 and when
a<1. -
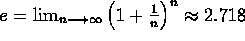 .
. -
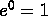 .
. -
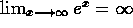 .
. -
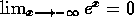 .
.
- Exponential Models
- Exponential growth:
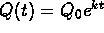 , k>0.
, k>0. - Exponential decay:
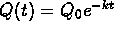 , k>0.
, k>0. - Learning curves:
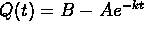 , A,B,k>0.
, A,B,k>0. - Logistic curves:
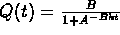 , A,B,k>0.
, A,B,k>0.
- The Natural Logarithm
-
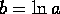 means
means 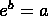 .
. -
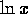 is only defined for x>0.
is only defined for x>0. -
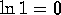 .
. -
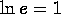 .
. -
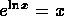 .
. -
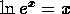 .
. - The graph of
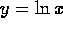 is obtained by reflecting the graph of
is obtained by reflecting the graph of
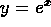 across the line y=x.
across the line y=x. -
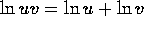 .
. -
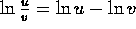 .
. -
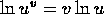 .
. -
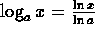 .
.
- Differentiation of Logarithmic and Exponential Functions
-
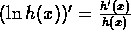 .
. -
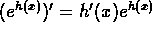 .
. - If
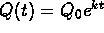 then Q'(t)=kQ(t) and
then Q'(t)=kQ(t) and
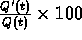 is the constant percentage 100k.
is the constant percentage 100k. - Logarithmic differentiation.
- Interest
- Simple interest: no interest is earned on any interest.
B(t)=P(1+rt).
- Compound interest, k times each year:
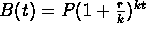 .
. - Continuously compounded interest:
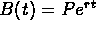 .
. - Effective interest rate:
- For interest compounded k times each year:
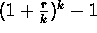 (as a decimal).
(as a decimal). - For interest compounded continuously:
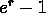 (as a decimal).
(as a decimal).
- The present value of B dollars payable t years from now is
 or
or 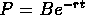 .
. - The present value of an annuity that consists of a periodic
sequence of payments over a specified term is the amount of money that
must be deposited today to permit periodic withdrawals generating the
same sequence of payments over the specified term, after which nothing
will be left in the account.
- Optimal holding time: When the percent rate of growth of the value of
an asset ceases to be greater than the prevailing interest rate, and begins
to be less than the prevailing interest rate. Equivalently, when the
present value of the value of the asset is greatest.
- Amortization of debt:
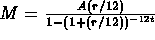 .
A is the amount of the loan, r is the interest rate (in decimal),
t is the number of years, M is the monthly payment.
.
A is the amount of the loan, r is the interest rate (in decimal),
t is the number of years, M is the monthly payment.



Next: About this document
Carl Lee
Tue Nov 10 08:47:50 EST 1998
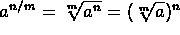 .
.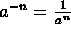 .
.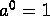 if
if 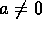 .
.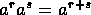 .
.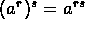 .
.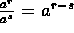 .
.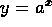 looks like when a>1 and when
a<1.
looks like when a>1 and when
a<1.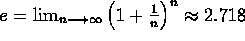 .
.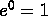 .
.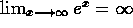 .
.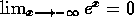 .
.
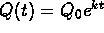 , k>0.
, k>0.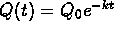 , k>0.
, k>0.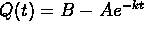 , A,B,k>0.
, A,B,k>0.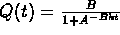 , A,B,k>0.
, A,B,k>0.
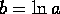 means
means 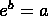 .
.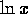 is only defined for x>0.
is only defined for x>0.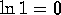 .
.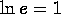 .
.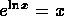 .
.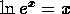 .
.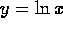 is obtained by reflecting the graph of
is obtained by reflecting the graph of
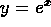 across the line y=x.
across the line y=x.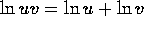 .
.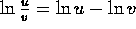 .
.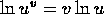 .
.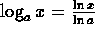 .
.
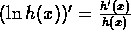 .
.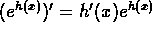 .
.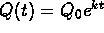 then Q'(t)=kQ(t) and
then Q'(t)=kQ(t) and
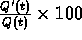 is the constant percentage 100k.
is the constant percentage 100k.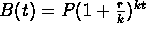 .
.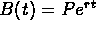 .
.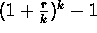 (as a decimal).
(as a decimal).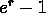 (as a decimal).
(as a decimal).
 or
or 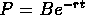 .
.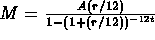 .
A is the amount of the loan, r is the interest rate (in decimal),
t is the number of years, M is the monthly payment.
.
A is the amount of the loan, r is the interest rate (in decimal),
t is the number of years, M is the monthly payment.