


Next: About this document
MA310 Homework #1
Due Monday, January 25
- Let's explore what happens when the leading coefficient in a
quadratic equation approaches zero.
Consider the function
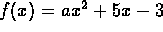 .
.
- Graphical exploration: On the same coordinate
system draw the graph of this function for several values of a
between -4 and 4. What is happening to the graph as a
approaches zero? What is happening to the x-intercepts?
- Algebraic analysis: As a approaches zero, the formula for
f(x) approaches g(x)=5x-3. What is the x-intercept for g(x)?
Prove algebraically that one of the x-intercepts for f(x) (i.e.,
one of the solutions for the quadratic equation f(x)=0) approaches
the x-intercept for g(x) as a approaches
zero.
- General algebraic analysis: Given a general quadratic equation
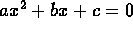 where
where 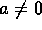 , prove that one of the solutions approaches the solution
to bx+c=0 as a approaches zero. For convenience, assume that
b>0.
, prove that one of the solutions approaches the solution
to bx+c=0 as a approaches zero. For convenience, assume that
b>0.
- In this problem we try to find a formula for the square root of
a general complex number.
- Find all square roots of i.
- Every complex number a+bi can be represented as a point
P=(a,b) in the plane. Assume
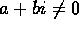 .
Let
.
Let 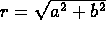 and let
and let 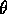 be the
angle from the positive x-axis to the ray OP, where O is the origin.
Explain why
be the
angle from the positive x-axis to the ray OP, where O is the origin.
Explain why 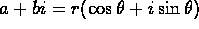 .
. - Suppose you want to multiply
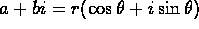 by
by
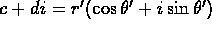 . Prove that the product is
. Prove that the product is
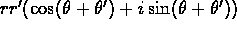 . (I.e., to multiply
two complex numbers, multiply their ``lengths'' and add their
``angles..'')
(Hint: Do you remember
your trigonometric angle addition formulas?)
. (I.e., to multiply
two complex numbers, multiply their ``lengths'' and add their
``angles..'')
(Hint: Do you remember
your trigonometric angle addition formulas?) - Prove that one square root of
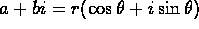 is
is 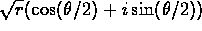 . What is the other
square root? How can you find you find them graphically?
. What is the other
square root? How can you find you find them graphically? - Find all square roots of 1+i. Express your final answer
without using sines and cosines. (Hint: Do you remember your
trigonometric half-angle formulas?)
- Find a general formula for the square roots of a+bi in terms
of a and b. For convenience, assume that
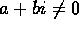 and
and
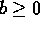 . Suggestion:
Use the half-angle formulas and the fact that
. Suggestion:
Use the half-angle formulas and the fact that
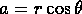 and
and 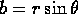 . Confirm your answer by squaring
it.
. Confirm your answer by squaring
it.



Next: About this document
Carl Lee
Wed Jan 27 08:17:21 EST 1999
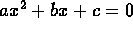 where
where 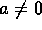 , prove that one of the solutions approaches the solution
to bx+c=0 as a approaches zero. For convenience, assume that
b>0.
, prove that one of the solutions approaches the solution
to bx+c=0 as a approaches zero. For convenience, assume that
b>0.
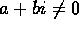 .
Let
.
Let 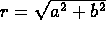 and let
and let 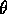 be the
angle from the positive x-axis to the ray OP, where O is the origin.
Explain why
be the
angle from the positive x-axis to the ray OP, where O is the origin.
Explain why 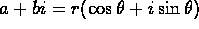 .
.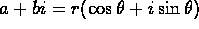 by
by
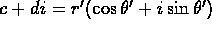 . Prove that the product is
. Prove that the product is
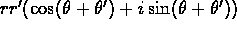 . (I.e., to multiply
two complex numbers, multiply their ``lengths'' and add their
``angles..'')
(Hint: Do you remember
your trigonometric angle addition formulas?)
. (I.e., to multiply
two complex numbers, multiply their ``lengths'' and add their
``angles..'')
(Hint: Do you remember
your trigonometric angle addition formulas?)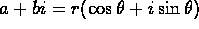 is
is 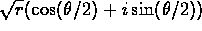 . What is the other
square root? How can you find you find them graphically?
. What is the other
square root? How can you find you find them graphically?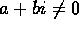 and
and
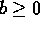 . Suggestion:
Use the half-angle formulas and the fact that
. Suggestion:
Use the half-angle formulas and the fact that
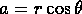 and
and 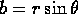 . Confirm your answer by squaring
it.
. Confirm your answer by squaring
it.