Polygonal Ears

A convex polygon with n sides can be dissected (triangulated) into triangles by drawing a certain number of non-crossing diagonals.

1. How many diagonals are needed?
2. How many triangles result?
3. A triangle in the triangulation consisting of two consecutive edges of the boundary together with one internal diagonal is called an ear of the triangulation. Prove that if 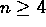then every triangulation has at least two ears.