Various Loci

1. Let 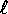be a horizontal line in the plane and F(r,s) be a point not on that line. Let e>0 be a positive real number. Find an equation to describe all points P(x,y) such that the ratio of PF divided by the distance from P to 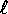equals e. What kind of curves do you get?
2. Let Q(-c,0) and R(c,0) be given points on the x-axis. Find an equation to describe all points P(x,y) such that the sum of the distances PQ+PR is a constant. What kind of curves do you get?
3. Let Q(-c,0) and R(c,0) be given points on the x-axis. Find an equation to describe all points P(x,y) such that the difference of the distances PQ-PR is a constant. What kind of curves do you get?
4. A wagon sits at the point (0,L) and a child stands at the point (0,0), holding a rope of length L attached to the wagon. The child begins walking along the positive x-axis, pulling the wagon along with the rope. Find an equation to describe the curve that the wagon follows.
5. A wheel of radius a rolls along the positive x-axis. There is a point P on the circumference of the wheel that initially touches the x-axis at the origin. Describe the curve traced out by P(x,y) as the wheel rolls, giving x and y in terms of the angle t about which the wheel has turned about its center. (Initially t=0. When P comes to rest on the x-axis again, .)
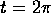6. A string is wound tightly many times around a circle of radius a centered at the origin. The end of the string is initially at the point (a,0). Describe the curve traced out by the end P(x,y) of the string as it is unwound, keeping the string taut. Let's assume that it is unwound in a counterclockwise direction. Suggestion: express the location of the point P in polar coordinates. Initially 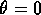and r=a.