


Next: Intersecting Circles
Up: Problems
Previous: More Handshaking
Quite simply, the Pigeonhole Principle states that if |X|>|Y|, then
there are no one-to-one functions from X into Y. So if m>n and
there are m pigeons and n pigeonholes in which they roost, there
must be at least one pigeonhole with more than one pigeon.
This obvious principle can be used to prove some perhaps
less-than-obvious facts.
- Prove that there are at least two humans on earth with the same number of
hairs on their heads.
- There are 100 people at a party. Assume that if person A
knows person B, then person B knows person A. Prove that there
are at least two people at the party who know the same number of
people.
- In a bureau drawer there are 60 socks, all identical except for
their color: 10 pairs are red, 10 are blue, and 10 are green. The
socks are all mixed up in the drawer, and the room the bureau is in is
totally dark. What is the smallest number of socks you must remove to
be sure you have at least one matching pair?
- Prove that when a fraction a/b is expressed in decimal form,
the resulting number will be either a terminating decimal or one that
repeats with a period no longer than b.
- Prove that if five points are placed anywhere on or in a square
of side length 1, at least two points will be no farther apart than
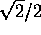 .
. - Prove that if five points are placed anywhere on or in an
equilateral triangle of side length 1, at least two points will be no
farther apart than 1/2.
- Try counting the edges around the faces of a polyhedron. You
will find that there are always two faces somewhere
bounded by the same number of
edges. Why?
- Prove that no matter how a set S of 10 positive integers
smaller than 100 is chosen there will always be two completely
different selections from S that have the same sum. For example, in
the set 3, 9, 14, 21, 26, 35, 42, 59, 63, 76 there are
the selections 14, 63, and 35, 42, both of which add to 77;
similarly, the selection 3, 9, 14 adds up to 26, a number that
is a member of the set.
- A physician testing a new medication instructs a test patient to
take 48 pills over a 30-day period. The patient is at liberty to
distribute the pills however he likes over this period as long as he
takes at least one pill a day and finishes all 48 pills by the end
of the 30 days. Prove that no matter how the patient decides to
arrange things, there will be some stretch of consecutive days in
which the total number of pills taken is 11.
- Suppose some set of 101 numbers
 is chosen from the numbers
is chosen from the numbers 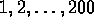 . Prove that it is
impossible to choose such a set without taking two numbers for which one
divides the other evenly; that is, with no remainder.
. Prove that it is
impossible to choose such a set without taking two numbers for which one
divides the other evenly; that is, with no remainder. - Consider a circle C with a radius of 16 and an annulus, or
ring, A, with an outer radius of 3 and an inner radius of 2.
Prove that wherever one might sprinkle a set S of 650 points inside
C the annulus A can always be placed on the figure so that it
covers at least 10 of the points.
- The next example concerns a marching band whose members are
lined up in a rectangular array of m rows and n columns. Viewing
the band from the left side, the bandmaster notices that some of the
shorter members are hidden in the array. He rectifies this aesthetic
flaw by arranging the musicians in each row in nondecreasing order of
height from left to right, so that each one is of height greater than
or equal to that of the person to his left (from the viewpoint of the
bandmaster). When the bandmaster goes around to the front, however,
he finds that once again some of the shorter members are concealed.
he proceeds to shuffle the musicians within their columns so that they
are arranged in nondecreasing order of height from front to back. At
this point he hesitates to go back to the left side to see what this
adjustment has done to his carefully arranged rows. When he does go,
however, he is pleasantly surprised to find that the rows are still
arranged in nondecreasing order of height from left to right!
Shuffling an array within its columns in this manner does not undo the
nondecreasing order in its rows. Can you prove this?
- Take the numbers from
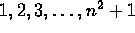 and arrange them in a
sequence in any order. Prove that when the arrangement is scanned
from left to right, it must contain either an increasing subsequence
of length (at least) n+1 or a decreasing subsequence of length (at
least) n+1. For example, when n=3, the arrangement
6,5,9,3,7,1,2,8,4,10 includes the decreasing subsequence 6,5,3,1.
(As this example demonstrates, a subsequence need not consist of
consecutive elements of the arrangement.)
and arrange them in a
sequence in any order. Prove that when the arrangement is scanned
from left to right, it must contain either an increasing subsequence
of length (at least) n+1 or a decreasing subsequence of length (at
least) n+1. For example, when n=3, the arrangement
6,5,9,3,7,1,2,8,4,10 includes the decreasing subsequence 6,5,3,1.
(As this example demonstrates, a subsequence need not consist of
consecutive elements of the arrangement.) - A lattice point is a point in a coordinate plane for which both
coordinates are integers. Prove that no matter what five lattice
points might be chosen in the plane at least one of the segments that
joins two of the chosen points must pass through some lattice point in
the plane.
- Six circles (including their circumferences and interiors) are
arranged in the plane so that no one of them contains the center of
another. Prove that they cannot have a point in common.
- Prove that in any row of mn+1 distinct real numbers there must
be either an increasing subsequence of length (at least) m+1 or a
decreasing subsequence of length (at least) n+1.



Next: Intersecting Circles
Up: Problems
Previous: More Handshaking
Carl Lee
Wed Apr 21 08:26:07 EDT 1999