Syllabus for MA 310-003
Mathematical Problem Solving for Teachers
(For Secondary School Majors)
Spring 1999
Course: MA 310-003, MWF 9:00-9:50, CB 337
Instructor: Carl Lee
Office: 967 Patterson Office Tower
Phone: 257-1405 (or 257-3336 to leave a message)
Email: lee@ms.uky.edu
Web Page: http://www.ms.uky.edu/~lee
Office Hours: MW 2-2:50, F 1-1:50, and by appointment. Occasionally the office hours will be cancelled because of a committee meeting, so you might want to check ahead before coming.
Prerequisites: MA 123 or MA 113.
Text: There is no text for the course, but from time to time I may assign readings on reserve in the library. I may decide to ask members of the class to purchase the book How to Solve it by Polya; if so, I will inform the class of the necessary arrangements.
Calculator: A graphic calculator, such as the TI-83, will sometimes be helpful.
Homework: There will be frequent homework assignments, but not on a set schedule.
Exams: At this point I am planning to have two or three exams exams during the semester.
Final Exam: Monday, May 3, 1:00 pm, in our regular room.
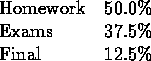
Grading:
Working Together: It is ok to work together on homework. However, when it comes time for you to write up the solutions, I expect you to do this on your own, and it would be best for your own understanding if you put aside your notes from the discussions with your classmates and wrote up the solutions entirely from scratch. Working together on exams, of course, is expressly forbidden.
Absences: A University excuse from a scheduled class activity such as an exam must be presented in writing no later than two weeks prior to the date of the absence. An absence due to illness or family emergency may be excused, provided that you can supply acceptable written evidence if required, and that you notify me as soon as possible. Notification is almost always possible immediately upon occurrence of an emergency. If you're too sick to telephone, you can get a friend to do it. Failure to make such timely notification may result in denial of your request. For an explanation of valid excused absences, refer to U.K.'s Student Rights and Responsibilities.
Cheating: The University's minimum penalty for cheating or plagiarism is a failure in the course. Cheating or plagiarism can lead to expulsion from the university. See Student Rights and Responsibilities for information on cheating, plagiarism, and penalities. It's not worth it, so don't do it.
Expectations: I expect that everyone will maintain a classroom conducive to learning. I like an informal atmosphere, but it must be orderly. Thus, everyone is expected to behave with basic politeness, civility, and respect for others. In particular, talking in class is ok if it's part of a class discussion or directed to me. Private communications are not, especially during quizzes and tests. Neither are reading extraneous materials, using electronic equipment, or sleeping.
Suggestions: Suggestions for improvement are welcome at any time. Any concern about the course should be brought first to my attention. Further recourse is available through the offices of the Department Ombud and the Department Chair, both accessible from the Main Office in 715 Patterson Office Tower.
Course Content:
My desires are well reflected in this statement of Polya from the introduction to his book How to Solve it:
A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. Such experiences at a susceptible age may create a taste for mental work and leave their imprint on mind and character for a lifetime.Thus, a teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking.
Also a student whose college curriculum includes some mathematics has a singular opportunity. This opportunity is lost, of course, if he regards mathematics as a subject in which he has to earn so and so much credit and which he should forget after the final examination as quickly as possible. The opportunity may be lost even if the student has some natural talent for mathematics because he, as everybody else, must discover his talents and tastes; he cannot know that he likes raspberry pie if he has never tasted raspberry pie. He may manage to find out, however, that a mathematics problem may be as much fun as a crossword puzzle, or that vigorous mental work may be an exercise as desirable as a fast game of tennis. Having tasted the pleasure in mathematics he will not forget it easily and then there is a good chance that mathematics will become something for him: a hobby, or a tool of his profession, or his profession, or a great ambition.
The author remembers the time when he was a student himself, a somewhat ambitious student, eager to understand a little mathematics and physics. He listened to lectures, read books, tried to take in the solutions and facts presented, but there was a question that disturbed him again and again. ``Yes, the solution seems to work, it appears to be correct; but how is it possible to invent such a solution? Yes, this experiment seems to work, this appears to be a fact; but how can people discover such facts? And how could I invent or discover such things by myself?'' Today the author is teaching mathematics in a university; he thinks or hopes that some of his more eager students ask similar questions and he tries to satisfy their curiosity. Trying to understand not only the solution of this or that problem but also the motives and procedures of the solution, and trying to explain these motives and procedures to others, he was finally led to write the present book. He hopes that it will be useful to teachers who wish to develop their students' ability to solve problems, and to students who are keen on developing their own abilities.