


Next: Finite Differences
Up: Tools
Previous: Another Summation Formula
When proving that a statement P(n) holds for all positive
integers 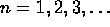 , two steps are necessary:
, two steps are necessary:
- First prove that the statement is
true when n=1.
- Second prove that the truth of the
statement for n=k+1,
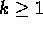 , follows from the truth of the
statement for n=k. (Alternatively, prove that the truth of the
statement for n=k+1 follows from the truth of the statement for
, follows from the truth of the
statement for n=k. (Alternatively, prove that the truth of the
statement for n=k+1 follows from the truth of the statement for
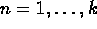 .)
.)
Example 1: Prove that 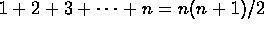 .
.
- Set n=1. Then 1=1(1+1)/2, so the
statement is true for n=1.
- Assume that the statement
is true for n=k (this is called the induction hypothesis). So
we assume that
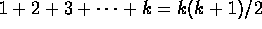 . Prove that the
statement is true for n=k+1. So we want to prove that
. Prove that the
statement is true for n=k+1. So we want to prove that
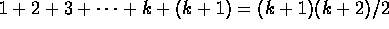 . We can do this as
follows:
. We can do this as
follows:
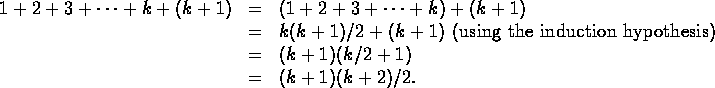
Therefore by mathematical induction, the
formula has been proved.
Example 2: Prove that the number of subsets of an
n-element set is 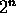 . For convenience, assume that the set
is
. For convenience, assume that the set
is 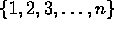 .
.
- Set
n=1. Then the number of subsets of the set
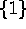 is
is
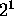 , so the statement is true for n=1.
, so the statement is true for n=1. - Assume that
the statement is true for n=k. So we assume that the number of
subsets of the set
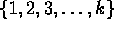 is
is 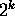 . Prove
that the statement is true for n=k+1. So we want to prove that
the number of subsets of the set
. Prove
that the statement is true for n=k+1. So we want to prove that
the number of subsets of the set 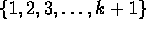 is
is
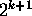 . We can do this as follows: Every subset of
. We can do this as follows: Every subset of
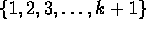 is one of two types: (1) Those
that do not contain the element k+1, and (2) those that do
contain the element k+1. The subsets of type (1) are all
subsets of
is one of two types: (1) Those
that do not contain the element k+1, and (2) those that do
contain the element k+1. The subsets of type (1) are all
subsets of 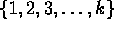 , so by the induction
hypothesis there are
, so by the induction
hypothesis there are 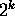 of them. The subsets of type (2) are
all subsets of the form
of them. The subsets of type (2) are
all subsets of the form 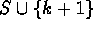 , where S is a
subset of
, where S is a
subset of 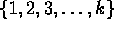 . By the induction
hypothesis there are
. By the induction
hypothesis there are 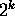 such subsets S, so there are
such subsets S, so there are 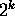 subsets of type (2). So altogether, the number of subsets of
subsets of type (2). So altogether, the number of subsets of
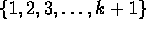 is
is 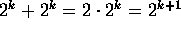 .
.
Therefore by mathematical induction, the
statement has been proved.
Look at pages 114-121 in the book How to Solve It to see another
explanation of mathematical induction and other examples.



Next: Finite Differences
Up: Tools
Previous: Another Summation Formula
Carl Lee
Wed Apr 21 08:17:28 EDT 1999
![]() , two steps are necessary:
, two steps are necessary:
![]() .
.
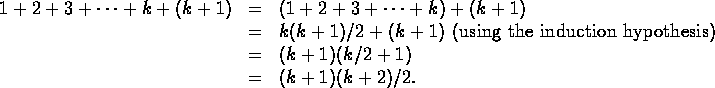
![]() . For convenience, assume that the set
is
. For convenience, assume that the set
is ![]() .
.