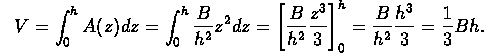Some general principles: Suppose 
and 
are two similar
figures. Assume that the ratio of two corresponding
one-dimensional lengths is a/b. Then the ratio of two corresponding
two-dimensional areas is 
, and the ratio of two corresponding
three-dimensional volumes is 
.
The volume of a prism with base of area B and height h is Bh (area of base times height).
The volume of a pyramid with base of
area A and height h is 
. You can prove this with
calculus by placing the pyramid with apex at the origin and
with base perpendicular to the
z-axis. Then we can calculate the volume by making slices
perpendicular to the z-axis. Let A(z) be the area of the slice
at position z. Then 
, so 
.
We get the volume by integrating from z=0 to z=h:
