


Next: About this document
MA341 HOMEWORK #5
Due Friday, October 15
Exam reminder: Our second exam will be on Wednesday, October 20.
The material covered will be everything since the last exam through
this homework assignment. Regarding material in the book: You should
learn and understand the definitions in Sections 2.6, 2.7, and 2.8.
- Use Geometer's Sketchpad to construct a regular hexagon starting
with the center and one vertex (corner) of the hexagon. You
may use only the following constructions: Line segments joining two
given points, circles with given center and point on the circle,
and points of intersection of two circles.
Include a brief written explanation of your steps.
If you are unable to get access to Geometer's Sketchpad, you may do
this construction with an actual compass and straightedge!
- Suppose
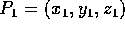 and
and
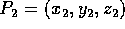 are two points in
are two points in 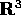 . Suppose that a is a real number
such that
. Suppose that a is a real number
such that 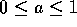 .
Let
.
Let 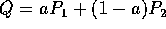 .
.
- Prove that
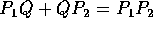 .
. - Prove that
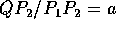 .
.
- Finish getting the coordinates of the icosahedron by finding
those twelve points on the sides of the octahedron. Suggestion: the
previous homework problem above shows how to get an arbitrary point on
the line segment between two given points, using a parameter a. Do
this for all twelve points using the same parameter a, and then
determine for what value of a the resulting shape will consist of
equilateral triangles. Make a good diagram and clearly label points
and their coordinates. Do NOT use decimal approximations; use exact
values (which will involve square roots).
Extra Credit: Use your coordinates to display the icosahedron using
Maple. The square root function in Maple is sqrt(). To display it
with proper proportions, use the command
polygonplot3d(icosahedron, scaling=constrained).
- Suppose R is an
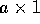 rectangle, where a>1. Let S be
the rectangle remaining when a
rectangle, where a>1. Let S be
the rectangle remaining when a 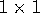 square is cut off of the end
of R. Assume the ratio of the length of S to the width of S is
the same as the ratio of the length of R to the width of R (i.e.,
the rectangles are proportional).
square is cut off of the end
of R. Assume the ratio of the length of S to the width of S is
the same as the ratio of the length of R to the width of R (i.e.,
the rectangles are proportional).
- Find a.
- What does a have to do with the icosahedron?
- Propose a topic for your video presentation. The presentation
itself will be 3-5 minutes long per person.



Next: About this document
Carl Lee
Thu Oct 7 13:17:52 EDT 1999
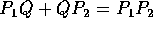 .
.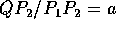 .
.