


Next: About this document
Some Review Notes
- Section 1.2.
- Concepts to know: Ordinary and Strong Induction.
- Look at Examples 1-7.
- Look at Problems 1-15.
- Chapter 1 Review.
- Look at the Review Problems and Summary on pages 39-40.
- Section 5.1.
- Concepts to know: graph, vertex, edge, loop, incident,
adjacent, parallel edges, simple graph, isomorphic graphs, complete
graph, bipartite graph, complete bipartite graph, directed graph,
weighted graph, degree, degree sequence, r-regular graph,
p, q,
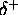 ,
,
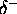 .
. - Proofs to know: Theorem 5.1, Corollary 1 to Theorem 5.1,
Corollary 2 to Theorem 5.1.
- Look at Puzzle 1, 2, 3(a), 4.
- Look at Problems 1-20.
- Section 5.2.
- Concepts to know: walk, path, trail, subgraph, connected,
component, connected graph, adjacency matrix, adjacency list.
- Look at Problems 1-8.
- Section 5.3.
- Concepts to know: circuit, cycle, Eulerian trail, Eulerian
circuit, Hamiltonian path, Hamiltonian cycle.
- Proofs to know: Theorem 5.2, Theorem 5.3, Theorem 5.4.
- Know how to find an Eulerian trail or circuit.
- Puzzles 1-4.
- Look at Problems 1-14.
- Section 5.4.
- Concepts to know: planar graph, plane graph, Euler's formula, r.
- Proofs to know: Theorem 5.6, Theorem 5.7.
- Theorems to know: Theorem 5.8.
- Look at Puzzle 1-2.
- Look at Example 1.
- Look at Problems 1-11.
- Section 5.5.
- Concepts to know: four-color problem,
chromatic number, chromatic polynomial.
- Proofs to know: Theorem 5.11.
- Theorems to know: Theorem 5.9, Theorem 5.10.
- Look at Puzzle 2.
- Look at Example 2.
- Look at Problems 1-10.
- Chapter 5 Review.
- Look at the Review Problems and Summary on pages 171-172.
- Section 6.1
- Concepts to know: Breadth First Search, length,
distance, Dijkstra's algorithm.
- Proofs to know: Theorem 6.3.
- Theorems to know: Theorem 6.1, Theorem 6.2.
- Look at Example 1.
- Look at Problems 1-10 in Section 6.1.
- Section 6.2.
- Concepts to know: tree, forest, spanning tree, Prüfer code.
- Proofs to know: Theorem 6.6, Corollary 2 to Theorem 6.6,
Theorem 6.8.
- Theorems to know: Theorem 6.4, Theorem 6.5, Corollary 1 to
Theorem 6.6, Theorem 6.7, Theorem 6.9.
- Look at Problems 1-15.
- Section 6.3.
- Concepts to know: directed tree, reachable, directed path, root,
rooted tree, branch, leaf, descendant, binary tree, ternary tree,
m-ary tree, regular m-ary tree, level, height, binary search,
minimum-weight tree, Prim's algorithm, Kruskal's algorithm, optimal
tree, Huffman's algorithm.
- Theorems to know: Theorem 6.10, Theorem 6.11.
- Look at Problems 1-10.
- Chapter 6 Review.
- Look at the Review Problems and Summary on pages 198-199.
- Section 10.2
- Concepts to know: activity network, earliest starting time
algorithm, critical path analysis, latest completion time, float time.
- Theorems to know: Theorem 10.4.
- Look at Example 2.
- Look at Problems 4-5.



Next: About this document
Carl Lee
Fri Apr 28 14:10:37 EDT 2000
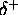 ,
,
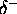 .
.