Matrices for Isometries in the Plane

>	with(linalg):

Develop the formula and the matrix for translating a point by the vector [a,b].

>	x2:=x1+a;  y2:=y1+b;

>	translate:=(a,b)->matrix([[1,0,a],[0,1,b],[0,0,1]]);

>	multiply(translate(a,b),[x,y,1]);

Develop the formula and the matrix for reflecting a point [x1,y1] over the line [a,b,c].

First, find the parametric equation of the line through [x1,y1] in the direction [a,b], and determine its intersection with the line [a,b,c]:

>	m:=expand([x1,y1]+t*[a,b]);

>	t1:=solve(a*(x1+t*a)+b*(y1+t*b)+c=0,t);

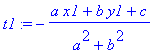
For convenience, assume a^2+b^2=1

>	t1:=-(a*x1+b*y1+c);

Now double t1 to find the reflected point.

>	expand([x1,y1]+2*t1*[a,b]);

>	reflect:=(a,b,c)->matrix([[1-2*a^2,-2*a*b,-2*a*c], [-2*a*b,1-2*b^2,-2*b*c],[0,0,1]]);

Develop the formula and the matrix for rotating a point about the origin by an angle x with sin(x)=s and cos(x)=c.

>	rotateaboutorigin:=(c,s)->matrix([[c,-s,0],[s,c,0],[0,0,1]]);

Develop the formula and the matrix for rotating a point about an arbitrary point [a,b] by an angle x with sin(x)=x and cos(x)=c.

>	rotate:=(a,b,c,s)->multiply(translate(a,b),rotateaboutorigin(c,s),translate(-a,-b));

>	rotate(a,b,c,s);

Check that the center of rotation is fixed.

>	multiply(rotate(a,b,c,s),[a,b,1]);

Develop the formula and the matrix for a glide reflection across the line [a,b,c] (with a^2+b^2=1) by the amount k.

>	glide:=(a,b,c,k)->multiply(translate(-b*k,a*k),reflect(a,b,c));

>	glide(a,b,c,k);

Any isometry can be thought of as a rotation or reflection that fixes the origin, followed by a translation.  Hence the upper 2x2 portion of any isometry matrix must consist of two perpendicular unit length vectors (an orthonormal 2x2 matrix).  Given any 3x3 matrix with an orthonormal upper-left 2x2 matrix and a last row consisting of [0,0,1], determine the type of isometry by testing the 2x2 determinant.  If it is 1, you have a translation or rotation.  If it is -1 you have a reflection or glide reflection.  

In the former case, you can determine c and s by inspection, and then must show you can always solve for a and b by checking the determinant of the coefficients of a and b in the last column when the angle is not zero:

>	det(matrix([[-c+1,s],[-s,-c+1]]));

This equals 2-2c which is only zero when c=1, corresponding to a rotation by an angle of zero.

If you have a reflection or glide reflection, you can solve for a and b (or their negatives) from the upper-left 2x2 matrix, and then must show you can always solve for c and k by checking the determinant of the coefficients of c and k in the last column:

>	det(matrix([[-2*a,-b],[-2*b,a]]));

This equals -2, which is not zero, so there is no problem.

Therefore, every such 3x3 matrix is a translation, rotation, reflection, or glide reflection.

>

>