


Next: About this document
Take-Home Exam #1
Due Thursday, October 8
You may refer to your class notes and ask me if you have questions,
but you are not permitted to use any other source of help or
discussion, whether human or nonhuman.
- Do problem #4 of Section 2.7 by induction.
- Finish the problem that we began in class: How many different
tetrahedra can be produced by coloring each face a solid color and
using n different colors? (Two tetrahedra are the same if they can be
turned and placed side by side so that corresponding sides match in color.)
So far, the numbers for n=0,1,2,3,4 are 0,1,5,15,36. Find and
prove a general formula.
-
- Use finite differences to guess a formula for
the sum of the fourth powers of the first n natural numbers.
- Work problem #4 of Section 3.8. However, there is a
correction. The final formula should read:
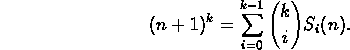
Then use the formulas in
problems #1, 5, and 6 of Section 2.7 for 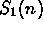 ,
, 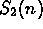 , and
, and 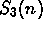 to derive the formula for
to derive the formula for 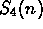 . Verify that you got the same
answer as in (a).
. Verify that you got the same
answer as in (a).
- Just to be certain everything is clear, give a concise
explanation for the formula for the number of injective functions from
X to Y if |X|<|Y|.
- Work problem #14 of Section 4.4. Suggestion: Consider the
oddness/evenness of each coordinate.
- Work problem #5 of Section 4.5.
- Work problem #9 of Section 4.5.
- Work problem #10 of Section 4.5.
Carl Lee
Wed Sep 30 08:09:45 EDT 1998
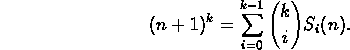
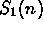 ,
, 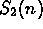 , and
, and 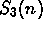 to derive the formula for
to derive the formula for 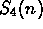 . Verify that you got the same
answer as in (a).
. Verify that you got the same
answer as in (a).