Take-Home Exam #2
Due Monday, December 14, 4:00 pm, in my mailbox, 745 POT

You may refer to your class notes and ask me if you have questions, but you are not permitted to use any other source of help or discussion, whether human or nonhuman. DO NOT TALK TO EACH OTHER ABOUT THESE EXAM QUESTIONS.

1. The Three Reflections Theorem. The purpose of this exercise is to prove the following: Suppose are two congruent triangles in the plane. Then with at most three reflections the points A,B,C can be moved to the points D,E,F, respectively. We will prove it in several stages.

   Remember that when a point P is reflected across a line , we find its image by first constructing a line m through P perpendicular to , then finding the point Q of intersection of the two lines, and finally finding the point R such that QR=QP and RP=2QP.

   In proving the following results, you may use the standard results in geometry about congruent triangles, perpendicular lines, isosceles triangles, etc. If you have any question about which theorems you may cite, just ask me.

   1. Suppose A and D are two different points in the plane. Prove that there is a line p such that the reflection of D across p is A.
   2. Suppose that A, B and E are three different points in the plane such that AB=AE. Prove that there is a line q such that the reflection of A across q is A, but the reflection of E across q is B.
   3. Suppose that A, B, C and F are four different points in the plane such that AC=AF and BC=BF. Prove that there is a line r such that the reflection of A across r is A, the reflection of B across r is B, but the reflection of F across r is C.
   4. Use the preceding three results to show that if 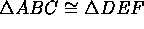are any two congruent triangles in the plane, then with at most three reflections the points A,B,C can be moved to the points D,E,F, respectively. Also, why might you sometimes need fewer than 3 reflections?
   5. Make a good conjecture (you do not have to prove it) about a result analogous to the three reflections theorem, involving two congruent tetrahedra in three-dimensional space.
   6. Extra Credit: Make a good illustration of the proof of the Three Reflections Theorem using Geometer's Sketchpad.

2. Semiregular Solids. Suppose is a space cluster (an ordered sequence q polygons meeting at a common point such that the sum of the interior angles is less than ). Suppose that this space cluster can be extended to enclose a polyhedron. For example, the space cluster (3,4,3,4) extends to enclose the cuboctahedron, which you already drew with Maple. It turns out that knowing only the cluster S we can figure out how many vertices (corners), edges, and polygons the polyhedron will have. This exercise explains how to do this.

   First, some definitions.

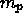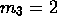   • Let denote the number of times the integer p appears in the cluster S. (For the cuboctahedron, and .)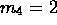
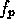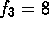   • Let denote the number of p-gons in the polyhedron. (For the cuboctahedron, and 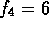(look at your pictures).)
   • Let f denote the total number of polygons of the polyhedron. (For the cuboctahedron, .)
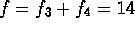   • Let v denote the number of vertices (corners) of the polyhedron. (For the cuboctahedron, v=12.
   • Let e denote the number of edges of the polyhedron. (For the cuboctahedron, e=24.
   1. Prove that 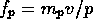. (Suggestion: Every vertex touches 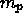p-gons, and every p-gon has p vertices.)
   2. Prove that e=qv/2. (Suggestion: Every edge has two vertices. How many edges does each vertex touch?)
   3. There is a wonderful theorem called Euler's Relation that states that

      

      Use this to prove that

      

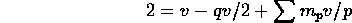
      where the sum is taken over all the different types of p-gons in S. Now explain why

      

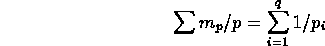
   4. Define

      

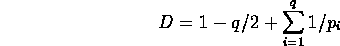
      Prove

      1. v=2/D.
      2. e=q/D.
      3. .
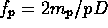   5. Use these formulas to find out how many vertices, edges, triangles, squares, and pentagons are in the polyhedron associated with the cluster (3,4,5,4).

• About this document ...