


Next: About this document
Homework #4
Due Thursday, September 17
- The Well-Ordering Property of Natural Numbers states: ``Every
nonempty subset S of the natural numbers has a smallest element.''
- Use the Axiom of Induction to prove the Well-Ordering Property.
Suggestion: Let S be any
subset of the natural numbers
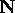 . Assume that S has no smallest
element. Let M be the complement of S. Prove that M
equals
. Assume that S has no smallest
element. Let M be the complement of S. Prove that M
equals 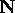 and hence that S must be empty.
and hence that S must be empty. - Use the Well-Ordering Property to prove the Axiom of Induction.
Suggestion: Let M be any subset of
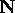 satisfying I and II
of the Axiom of Induction. Let S be the complement of M. Prove
that S is empty and hence that M must be
satisfying I and II
of the Axiom of Induction. Let S be the complement of M. Prove
that S is empty and hence that M must be 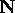 .
.
- Suppose there are m people,
m-1 black hats and m red hats. Assume individuals
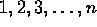 are given red hats and individuals
are given red hats and individuals
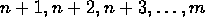 are given black hats. Each person in order
(
are given black hats. Each person in order
( 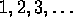 ) is asked in
turn whether or not he/she can deduce the color of his/her hat. Prove
by induction on n that person n can correctly deduce that his/her hat
is red.
) is asked in
turn whether or not he/she can deduce the color of his/her hat. Prove
by induction on n that person n can correctly deduce that his/her hat
is red. - Induction problems #8, 10 (you can use the result
of 9), 18.
- Be sure you know how to do induction problems
#2, 3, 4, 6, 9, 11, 12, but do not
hand them in.
Carl Lee
Thu Sep 10 08:15:17 EDT 1998
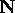 . Assume that S has no smallest
element. Let M be the complement of S. Prove that M
equals
. Assume that S has no smallest
element. Let M be the complement of S. Prove that M
equals 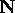 and hence that S must be empty.
and hence that S must be empty.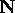 satisfying I and II
of the Axiom of Induction. Let S be the complement of M. Prove
that S is empty and hence that M must be
satisfying I and II
of the Axiom of Induction. Let S be the complement of M. Prove
that S is empty and hence that M must be 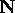 .
.