


Next: About this document
Homework #5
Due Tuesday, October 27
- Find all the cube roots of i.
- Draw any non-convex quadrilateral such that no two sides are the
same length. Draw an ``Escher-like'' tiling of the plane by modifying the
sides of this quadrilateral in the manner that we discussed in class.
You may use Geometer's Sketchpad to do this if you wish.
- Explain how you can be absolutely certain that we have found all
21 possible planar clusters. Some suggestions: What are the
possible numbers of polygons that can be in a cluster? For each
possible number, what are the possible numbers of triangles that can
be in a cluster? For each possible number of triangles, what are the
possible numbers of squares? Etc.
- Consider two points
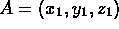 and
and 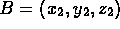 in
space.
in
space.
- What are the coordinates of the midpoint of the segment
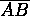 ?
? - Suppose we wish to divide the segment
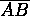 by a point
C such that AC:CB=3:2. Determine the coordinates of C.
by a point
C such that AC:CB=3:2. Determine the coordinates of C.
- Determine coordinates of the vertices of the polyhedron
determined by the space cluster 3-4-3-4. Use Maple to draw it.
Print out the result.
- Read the article on imaginary numbers and the two articles on
tilings that are on reserve in the Education Library.
You should have already done this:
- Make good drawings of the possible tilings by planar clusters.
- Find samples of border wallpaper and regular wallpaper with
interesting repeating patterns.
Carl Lee
Wed Nov 4 12:25:34 EST 1998
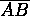 ?
?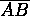 by a point
C such that AC:CB=3:2. Determine the coordinates of C.
by a point
C such that AC:CB=3:2. Determine the coordinates of C.