Here is a true story of a ninth-grader. He was thinking about the
game of Go which is played on a 
grid and was wondering
how many intersection points there were on the board. So he wanted to
know what 
was, but did not have a piece of paper handy. He
wondered if he could figure out how much needed to be subtracted from
to get . He mentally envisioned the following table:
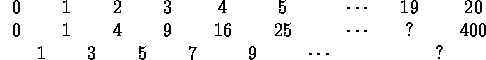
He saw that the square of n+1 was obtained by adding 2n+1 to the
square of n. Thus 
so 
.
Later, when he wrote this down, he recognized that he had simply rediscovered
the formula 
, which he had seen before. But now he
began to think of something else: When going from 
to 
the
amount added was 9, which just happened to be a perfect square. So
, which means that (4,3,5) is a Pythagorean triple.
Might not other Pythagorean triples be found this way? They can for
integer values of n for which 2n+1 is a perfect square. Or,
working backwards, start with a perfect square 
, set it equal to
2n+1, solve for n, and see if n is an integer. A little
reflection convinced him that this works if and only if m is odd.
In this case, 
and you have the Pythagorean triple
(m,n,n+1).
This gave him a method of generating some Pythagorean triples:
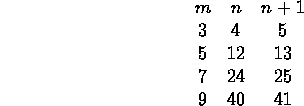
He noticed that not all Pythagorean triples were generated this way;
for example, the triple (6,8,10) would be absent. But he realized
he could make more triples using similar formulas. For example, he
could start with 
. If 4n+4 happened to be a
perfect square , then he could solve for n, getting 
and the triple (m,n,n+2). He realized that n would be an integer
if and only if m were even. So he generated more triples:
Finally, he generalized this procedure by using the formula
. If he started with a perfect square , set
it equal to 
, and solved for n, he got 
.
If n turns out to be an integer, the Pythagorean triple
(m,n,n+f) results. By choosing any number m, running through all
possibilities of f from 1 to m, he realized that all Pythagorean
triples starting with m could be found.
He wrote up this investigation as a science fair project, received the grand prize in his school and an honorable mention in his county.