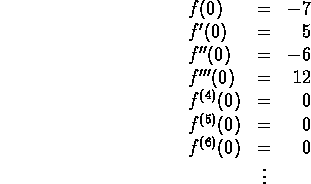
Suppose you are asked to find a function f(x) such that
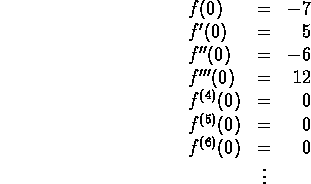
We might guess that the function is a polynomial of degree 3. How can we determine the coefficients?
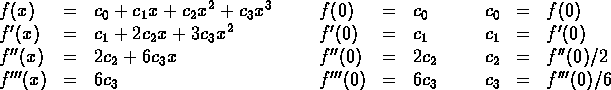
In our example, 
, 
, 
, and 
so
.
In general, if you think f(x) is a polynomial of degree m,
, then
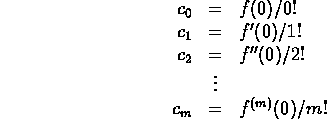
so
What is the number of different triangles you can form on a flat surface using three toothpicks for the three sides of each triangle, given an unlimited supply of toothpicks of n different colors?
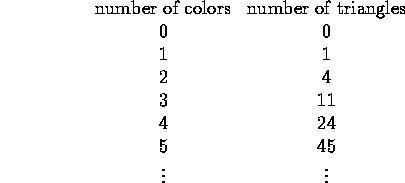
We want a formula f(n) so that
Look for a pattern by subtracting these numbers from each other, making a difference table:
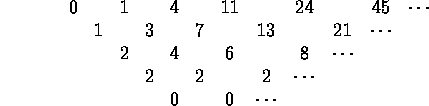
Consider some known formulas:
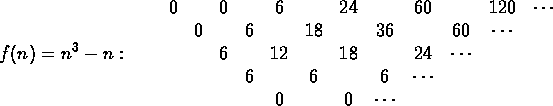
This suggests that for our problem we seek a formula of degree 3.
Let's call the numbers in the first row
and the numbers in the second row
and the numbers in the third row
etc. These aren't equal to derivatives in the sense of differential calculus, but there seems to be a strong analogy.
In differential calculus, we exploited;
What is the analog for differences? Define
This is sometimes called a falling factorial.
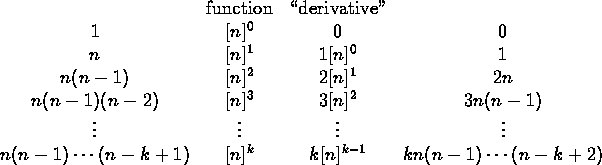
Verification:
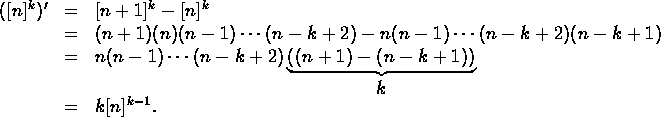
Now we can guess formulas:
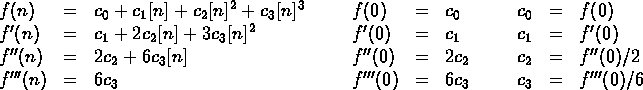
In our example,
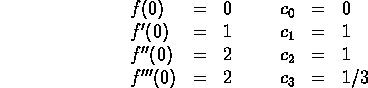
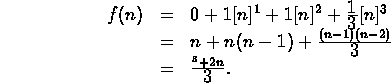
Now we have a formula that we can try to prove, e.g., by induction, or directly.
In general, fetch f(0), f'(0), f''(0), ..., 
as
the first entries of the rows of the difference table (assuming we
have reached a row of zeroes). Then
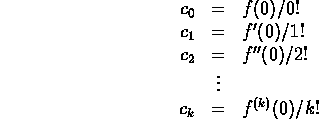
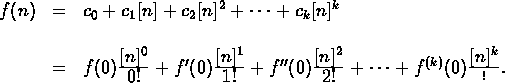
Note that
so
(taking 
if n<j).
In our example,
Here is another way of doing the same thing--via ``antiderivatives.''
and you can verify that this is equal to
,
which is the formula we had found before.