Playing around with series can give more techniques. Remember how to figure out the formula for geometric series like
We can keep this in mind as we tackle a ``Fibonacci''-like sequence:
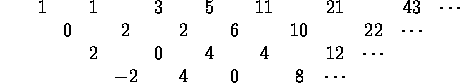
We never seem to get a row of zeroes. The second row ``looks like''
twice the first row; i.e., f(n+1)=f(n)+2f(n-1) for 
. (The
ordinary Fibonacci sequence satisfies f(n+1)=f(n)+f(n-1).)
Let define a power series using f(n) as the coefficient of 
:
The relationship f(n+1)-f(n)-2f(n-1)=0 suggests:
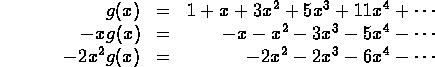
Remember, f(n) is the coefficient of . Let's try to find it.
We did the last step using the method of partial fractions. Continuing,
since we have geometric series.
So the coefficient of is
and this is our guess for the formula for f(n).
Exercise: Derive a formula for the ordinary Fibonacci sequence this way.