Some Counting Questions

When we write |X|=m, we mean that X is a finite set that contains exactly m elements; i.e., the cardinality of X is m.

1. If |X|=m and |Y|=n, how many relations between X and Y are there?
2. If |X|=m and |Y|=n, how many functions 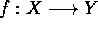are there?
3. Suppose |X|=m, |Y|=n, and 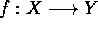is a function. Try to fill in the following table by giving a formula for the number of functions in each case:

   

4. How many ways are there of removing a regular tetrahedron from the table and replacing it in the same position, but not necessarily with the same sides facing the same directions as before?
5. How many ways are there of removing a cube from the table and replacing it in the same position, but not necessarily with the same sides facing the same directions as before?