


Next: Some Useful Tautologies
Up: Brief Logic
Previous: Brief Logic
From Wolf:
- A proposition is any declarative statement (including
mathematical sentences such as equations) that is true or false.
- We use the letters
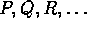 as propositional
variables. That is, we let these letters stand for or represent
statements.
as propositional
variables. That is, we let these letters stand for or represent
statements. - Five symbols, called connectives, are used to stand for
the following words:
-
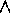 for ``and''. Conjunction.
for ``and''. Conjunction. -
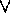 for ``or''. Disjunction.
for ``or''. Disjunction. -
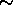 for ``not''. Negation.
for ``not''. Negation. -
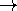 for ``implies'' or ``if...then''.
Conditional or Implication.
for ``implies'' or ``if...then''.
Conditional or Implication. -
 for ``if and only if''. Biconditional or
Equivalence.
for ``if and only if''. Biconditional or
Equivalence.
- A statement that is not built up from simpler ones by
connectives and/or quantifiers is called atomic or
simple. (Quantifiers will be introduced later.) A statement that
is built up from simpler ones is called compound.
- The truth functions of the connectives are defined as
follows:
-
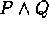 is true provided P and Q are both true.
is true provided P and Q are both true. -
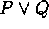 is true provided at least one of the statements P
and Q is true.
is true provided at least one of the statements P
and Q is true. -
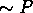 is true provided P is false.
is true provided P is false. -
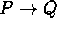 is true provided P is false, or Q is true (or
both).
is true provided P is false, or Q is true (or
both). -
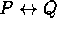 is true provided P and Q are both true or both
false.
is true provided P and Q are both true or both
false.
- A tautology, or a law of propositional logic, is a
statement whose truth function has all T's as outputs.
- A contradition is a statement whose truth function has
all F's as outputs (in other words, it's a statement whose negation
is a tautology).
- Two statements
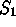 and
and 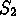 are called
propositionally equivalent if
are called
propositionally equivalent if 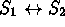 is a tautology.
is a tautology.
Carl Lee
Wed Nov 18 12:16:44 EST 1998
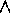 for ``and''. Conjunction.
for ``and''. Conjunction.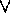 for ``or''. Disjunction.
for ``or''. Disjunction.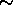 for ``not''. Negation.
for ``not''. Negation.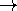 for ``implies'' or ``if...then''.
Conditional or Implication.
for ``implies'' or ``if...then''.
Conditional or Implication. for ``if and only if''. Biconditional or
Equivalence.
for ``if and only if''. Biconditional or
Equivalence.
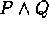 is true provided P and Q are both true.
is true provided P and Q are both true.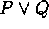 is true provided at least one of the statements P
and Q is true.
is true provided at least one of the statements P
and Q is true.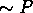 is true provided P is false.
is true provided P is false.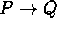 is true provided P is false, or Q is true (or
both).
is true provided P is false, or Q is true (or
both).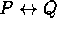 is true provided P and Q are both true or both
false.
is true provided P and Q are both true or both
false.