


Next: About this document
Up: Brief Logic
Previous: Some Problems
From Wolf:
- A mathematical variable is a symbol (or combination of
symbols like
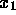 ) that stands for an unspecified number or other
object. The collections of objects from which any particular variable
can take its values is called the domain or universe
of that variable. Variables with the same domain are said to be of
the same sort.
) that stands for an unspecified number or other
object. The collections of objects from which any particular variable
can take its values is called the domain or universe
of that variable. Variables with the same domain are said to be of
the same sort. - Two symbols, called quantifiers, stand for the following
words:
-
 for ``for all'' or ``for every'' or ``for any''.
Universal quantifier.
for ``for all'' or ``for every'' or ``for any''.
Universal quantifier. -
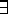 for ``there exists'' or ``there is'' or ``for some''.
Existential quantifier.
for ``there exists'' or ``there is'' or ``for some''.
Existential quantifier.
- The quantifiers are used in symbolic mathematical language as
follows: If P is any statement, and x is any mathematical
variable (not necessarily a real number variable), then
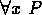 and
and 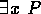 are also statements. In this case we say that x
is quantified.
are also statements. In this case we say that x
is quantified. - A mathematical variable occurring in a symbolic statement is
called free if it is unquantified and bound if it is
quantified. If a statement has no free variables it's called
closed. Otherwise it's called a predicate, an open
sentence, an open statement, or a propositional function.
- A statement of the form
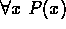 is defined to be true
provided P(x) is true for each particular value of x from its
domain. Similarly,
is defined to be true
provided P(x) is true for each particular value of x from its
domain. Similarly, 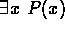 is defined to be true provided
P(x) is true for at least one value of x from that domain.
is defined to be true provided
P(x) is true for at least one value of x from that domain. - For any statement P(x),
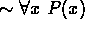 is logically
equivalent to
is logically
equivalent to 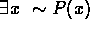 . Also,
. Also, 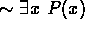 is
logically equivalent to
is
logically equivalent to 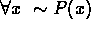 .
. - Let P be any statement, x be any mathematical variable, and
t any term that denotes a set. (So t could be a single letter
standing for a set, or a more complicated expression like
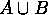 .)
Then
.)
Then
-
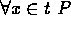 is an abbreviation for
is an abbreviation for 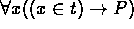 .
. -
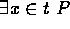 is an abbreviation for
is an abbreviation for 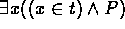 .
.
Carl Lee
Wed Nov 18 12:16:44 EST 1998
 for ``for all'' or ``for every'' or ``for any''.
Universal quantifier.
for ``for all'' or ``for every'' or ``for any''.
Universal quantifier. for ``there exists'' or ``there is'' or ``for some''.
Existential quantifier.
for ``there exists'' or ``there is'' or ``for some''.
Existential quantifier.
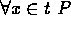 is an abbreviation for
is an abbreviation for 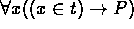 .
.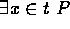 is an abbreviation for
is an abbreviation for 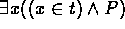 .
.