


Next: About this document
Problem Solving Examples
Carl Lee
- Generalizing, Specializing, and Analogy
- The Pythagorean Theorem states that if we erect squares on the three
sides of a right triangle, the sum of the areas of the squares on
the legs equals the area of the square on the hypotenuse.
What if we erect equilateral triangles or semicircles instead?
What is the ``right'' shape to consider?
- Into how many parts can space be divided by six planes?
- Isomorphic Problems
- Onto a
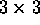 ``chessboard'' four knights are placed: a black
knight on each of the two upper corners, and a white knight on each
of the two lower corners. Using standard knight moves, interchange
the black knights with the white knights in as few moves as
possible.
``chessboard'' four knights are placed: a black
knight on each of the two upper corners, and a white knight on each
of the two lower corners. Using standard knight moves, interchange
the black knights with the white knights in as few moves as
possible. - If in the above problem, one of the white knights is replaced with a
red knight, exchange the white and red knights in as few moves as
possible.
- Here is a game called ``fifteen.'' The numbers from one to nine are
written on a piece of paper. There are two players, one with a
supply of pennies, the other with a supply of dimes. The players
take turns covering a number with one of their coins. The winner
is the one whose covered numbers include three different numbers
summing to fifteen. What is the best strategy for this game?
- You have three flasks with volumes 12, 7 and 5
gallons, respectively. There are no markings on the flasks.
The 12 gallon flask is filled with water. The problem is to
pour the water back and forth among the flasks so that eventually
the 12 gallon flask and the 7 gallon flask each contains
exactly 6 gallons of water.
- How many monomials of the form
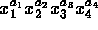 are there of degree 8? Each
are there of degree 8? Each 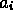 must be a nonnegative integer.
must be a nonnegative integer.
- Enlarging the Feasible Region
- Using six toothpicks, form four equilateral triangles. The length of the
sides of each triangle is the same: the length of a toothpick.
- Three shipwrecked sailors gather coconuts, agreeing to divide them in
the morning. During the night, the sailors get greedy.
One by one, each gets up, divides the coconuts into three equal
piles with one coconut left over, which is thrown to a monkey.
He takes and hides a pile, and pushes the remaining two piles
together and leaves. In the morning, they all get together,
divide the remaining coconuts into three equal piles with one
coconut left over, which they throw to the monkey. How many
coconuts were gathered initially?
- Everyone has seen straight swords that fit into straight scabbards
and curved swords that fit into curved scabbards. Can you think
of any other shapes that work?
- Find a way of dissecting a square of unit area into a finite number
of pieces which can be reassembled to form a solid ``plus''
sign of unit area.
- Invoking Continuity
- Show that a perfect square can be inscribed about Lake Michigan.
- There is a long path up the side of a mountain. At 7:00 on Monday
morning, a hiker begins climbing the mountain using this path.
She often stops for rests, sometimes walks back along the path
for a while before resuming her climb, and finally reaches the
top of the mountain at 7:00 in the evening. She spends the night
at the top of the mountain. At 7:00 on Tuesday morning, she
begins her trip back down the mountain, again using the same
path. Again she hikes in a leisurely fashion, sometimes stopping,
sometimes backtracking, but finally reaching the bottom of the
mountain at 7:00 in the evening. Show that there is some time
between 7:00 a.m. and 7:00 p.m. so that at this time she was at
the same spot on the path on both days.
- Considering the Extreme Case
- The Tack Carpet Company was asked to provide wall-to-wall carpeting
for a ring shaped corridor in a new airport (i.e., bounded by
two concentric circles). When Mr. Tack saw the plans he was angry.
The only measurement given was the length of a chord that was
tangent to the inner wall: 100 meters.
He said, ``Confound it. How can I
give them an estimate of carpet cost when I don't know the area
of that ring between the two circles? I'd better go and see my
designer, Mr. Sharp.'' Mr. Sharp, a skilled geometer, wasn't
too upset. He said, ``That chord is the only length I asked for,
Mr. Tack. I just plug it into a formula I have and it gives the
ring's area.'' Mr. Tack looked surprised for a minute, then
smiled. He said, ``Thank you, Mr. Sharp, but I don't need you
or your formula. I don't have to know the areas of the two
circles either. I can give you the result immediately.''
Do you know how Mr. Tack did it?
- A cylindrical hole is drilled straight through the center of a solid
sphere. When measured, the length of the hole is found to be
six inches. What is the volume of the sphere that remains?
- Physical Analogy
- Suppose you know the formula
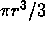 for the volume of a cone
whose height is r and the radius of whose base is also r.
Suppose you also know that the center of mass of such a cone is
at a distance of r/4 from the base. Derive the formula for
the volume of a sphere.
for the volume of a cone
whose height is r and the radius of whose base is also r.
Suppose you also know that the center of mass of such a cone is
at a distance of r/4 from the base. Derive the formula for
the volume of a sphere.
- Relating the Solutions of Several Problems
- A collection of mutually antagonistic knights placed on a chessboard
so that no knight can be captured by any other in one standard
knight's move is called independent. Show that the maximum
size of an independent set of knights that can be placed on an
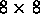 chessboard is 32. What is the size of a maximum
independent set of knights that can be placed on the following
size boards:
chessboard is 32. What is the size of a maximum
independent set of knights that can be placed on the following
size boards: 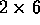 ,
, 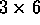 ,
, 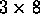 ,
,
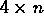 for
for 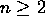 ?
? - Given a chessboard. A segment is a line connecting two cells
that are separated by exactly one standard knight's move.
A set of segments is a covering if every cell of the
chessboard is at the end of at least one segment in the set.
Show that the minimum size of a covering for an
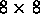 chessboard is 32. What is the size of a minimum covering on the
following size boards:
chessboard is 32. What is the size of a minimum covering on the
following size boards: 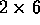 ,
, 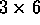 ,
, 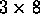 ,
,
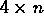 for
for 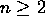 ?
? - Show that it is possible for a knight to tour an
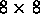 chessboard
using standard knight's moves in such a way that every square is
visited exactly once, the knight returning to its starting square.
Such a tour is called a knight's tour.
chessboard
using standard knight's moves in such a way that every square is
visited exactly once, the knight returning to its starting square.
Such a tour is called a knight's tour. - Show that the only way that 32 knights can be placed independently
on an
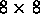 chessboard is by placing them all on squares
of the same color.
chessboard is by placing them all on squares
of the same color. - Show that
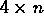 boards for
boards for 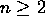 do not possess knight's
tours.
do not possess knight's
tours.
- Symmetry
- Two players alternately place non-overlapping
pennies on a square table. The
first person unable to place a penny loses. Can the first or the
second player always win this game? What is the winning strategy?
What if the game is played with cigars?
- Two players play a game of toe-tac-tic, which is the same as
tic-tac-toe, except that the first person to achieve three
in a row is the loser instead of the winner. Can the first
or the second player always win this game? What is the winning
strategy? What if the game is played on a
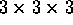 board?
board?
- Functional Fixedness
- Determine the height of a building using a barometer.
- There are two long strings that are hanging from the ceiling of an
empty room. They are so far apart that if you hold one end, you
can't reach the other. The problem is to tie the two ends together
using nothing more than a pair of scissors.
- Place an open bottle of water in the center of a small oriental rug.
The problem is to get the bottle off the rug. But you musn't
touch the bottle with any part of your body or anything else.
And, of course, not a drop of water must be spilled.
- You have a sheet of newspaper. The problem is for you and a friend
to stand on it in such a way that you can't touch each other.
Naturally, you can't step off the paper.
- You have a tennis ball. Try to throw it so it goes a short distance,
comes to a dead stop, then reverses itself and goes the opposite
way. You are not allowed to bounce it against something, and you
can't hit it with anything or tie anything to it.
- Finding a General Solution
- Try to form as many whole numbers as possible, starting with 1,
by using only the digit 4 four times--no more, no less--together
with simple mathematical symbols. Naturally one must establish
what is meant by a ``simple'' symbol. This traditionally
includes the arithmetic signs for addition, subtraction,
multiplication, and division, together with the square-root
sign (repeated as many finite times as desired), parentheses,
decimal points, and the factorial sign. A decimal point may also
be used to indicate a repeating decimal. What if ``log'' is
also allowed?
- Logic
- Three students are seated on a bench and told to close their eyes.
They are told by the teacher that she will put either a red or a blue
hat on each of them. They will then be asked to open their eyes.
Each will then raise his hand if he sees a red hat on someone else.
(They won't be able to see their own hats.)
The first person to deduce
the color of his own hat will win a prize.
Now in fact the teacher puts a red hat on each of them. Of course,
all three raise their hands. But several minutes passes before
one of them stands up and shouts, ``I know my hat is red.''
How did the winner figure it out? What would have happened if
there were four students, each with a red hat?
- ``I hear some youngsters playing in the back yard,'' said Jones,
a graduate student in mathematics. ``Are they all yours?''
``Heavens, no,'' exclaimed Professor Smith, the eminent number
theorist. ``My children are playing with friends from three
other families in the neighborhood, although our family
happens to be the largest. The Browns have a smaller number of
children, the Greens have a still smaller number, and the Blacks
the smallest of all.''
``How many children are there altogether?'' asked Jones. ``Let
me put it this way,'' said Smith. ``There are fewer than 18
children, and the product of the numbers in the four families
happens to be my house number which you saw when you arrived.''
Jones took a notebook and pencil from his pocket and started
scribbling. A moment later he looked up and said, ``I need
more information. Is there more than one child in the Black
family?'' As soon as Smith replied, Jones smiled and correctly
stated the number of children in each family. Knowing the house
number and whether the Blacks had more than one child, Jones
found the problem trivial. It is a remarkable fact, however,
that the number of children in each family can be determined
solely on the basis of the information given above! Can you
do it?
- Three men--A, B and C--are aware that all three of them are
``perfect logicians'' who can instantly deduce all the consequences
of a given set of premises. There are four red and four green
stamps available. The men are blindfolded and two stamps are
pasted on each man's forehead. The blindfolds are removed.
A, B and C are asked in turn: ``Do you know the colors of your
stamps?'' Each says: ``No.'' The question is then asked of
A once more. He again says: ``No.'' B is now asked the
question, and replies: ``Yes.'' What are the colors of B's
stamps?
- Counterintuitive Results
- You have the chance to play a game with three strangely numbered
dice. Die A is labeled with the numbers 1,2,11,12,15,16.
Die B is labeled with the numbers 5,6,9,10,13,14. Die C is
labeled with the numbers 3,4,7,8,17,18. There are two players.
The first player selects one of the dice. Then the second player
selects one of the dice. Each rolls his die, and the winner is the
one with the higher number. Would you rather go first or
second? What die would you choose?
- Geometry
- A pilot flies due south 100 kilometers, then goes east 100
kilometers, then north 100 kilometers and finds that he's
right back where he started from. Where did he start from?
How many correct answers are there to this problem?
- A pilot starts at the equator and flies due northeast. Where will
his flight end? How long is the path and what does it look like?
- A rectangle is inscribed in a circle of radius 9. The midpoints of
the four sides of the rectangle are joined to form a diamond.
What further information do you need to determine the length
of the sides of the diamond?
- Four bugs--A, B, C and D--occupy the corners of a square
10 inches on a side. A and C are male and are diagonally
opposite each other. B and D are female and are also diagonally
opposite each other. Simultaneously A crawls directly toward B, B
toward C, C toward D and D toward A. If all four bugs crawl at the
same constant rate, they will describe four congruent logarithmic
spirals which meet at the center of the square. How far does
each bug travel before they meet?
- Rates, Times and Distances
- There are two towns, conveniently called ``A'' and ``B'' joined by
a road. A businessman must drive from A to B, conduct
some business (what else?) and return to A. He wants his total
round trip speed to average 50 miles per hour, but he
encountered heavy traffic going to B and averaged only 25 miles
per hour on the first half of the trip. What should his average
speed be on the return trip to meet his goal?
- Two trains are traveling toward each other on the same track. Initially
they are 120 miles apart. One is traveling 25 miles per hour, and
the other is traveling 35 miles per hour. At the instant that they
are 120 miles apart, a fly sitting on the front of the first train
flies toward the second train at a speed of 40 miles per hour. The
moment it reaches the second train, it reverses direction and flies
back toward the first train. Again it reverses direction, and
continues to fly
back and forth between the two trains until the trains meet.
How far does the fly fly?



Next: About this document
Carl Lee
Mon Sep 14 12:19:48 EDT 1998
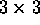 ``chessboard'' four knights are placed: a black
knight on each of the two upper corners, and a white knight on each
of the two lower corners. Using standard knight moves, interchange
the black knights with the white knights in as few moves as
possible.
``chessboard'' four knights are placed: a black
knight on each of the two upper corners, and a white knight on each
of the two lower corners. Using standard knight moves, interchange
the black knights with the white knights in as few moves as
possible.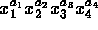 are there of degree 8? Each
are there of degree 8? Each 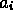 must be a nonnegative integer.
must be a nonnegative integer.
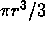 for the volume of a cone
whose height is r and the radius of whose base is also r.
Suppose you also know that the center of mass of such a cone is
at a distance of r/4 from the base. Derive the formula for
the volume of a sphere.
for the volume of a cone
whose height is r and the radius of whose base is also r.
Suppose you also know that the center of mass of such a cone is
at a distance of r/4 from the base. Derive the formula for
the volume of a sphere.
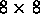 chessboard is 32. What is the size of a maximum
independent set of knights that can be placed on the following
size boards:
chessboard is 32. What is the size of a maximum
independent set of knights that can be placed on the following
size boards: 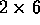 ,
, 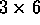 ,
, 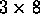 ,
,
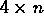 for
for 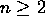 ?
?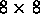 chessboard is 32. What is the size of a minimum covering on the
following size boards:
chessboard is 32. What is the size of a minimum covering on the
following size boards: 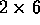 ,
, 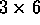 ,
, 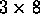 ,
,
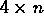 for
for 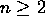 ?
?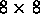 chessboard
using standard knight's moves in such a way that every square is
visited exactly once, the knight returning to its starting square.
Such a tour is called a knight's tour.
chessboard
using standard knight's moves in such a way that every square is
visited exactly once, the knight returning to its starting square.
Such a tour is called a knight's tour.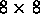 chessboard is by placing them all on squares
of the same color.
chessboard is by placing them all on squares
of the same color.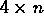 boards for
boards for 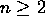 do not possess knight's
tours.
do not possess knight's
tours.
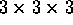 board?
board?