Example of the formula for coefficients of the non-square-free terms of a linear stress polynomial.

> with(linalg):

The simplicial complex has facets: 213, 143, 423, 125, 245, 415. Bipyramid over triangle 124.

The following are chosen for the coordinates of the vertices.

> v1:=[0,0,-1]; v2:=[2,0,1]; v3:=[0,1/2,1/2]; v4:=[-2,0,1]; v5:=[0,-1/2,1/2];

> M:=transpose(array([v1,v2,v3,v4,v5]));

The following is a linear 3-stress.

> b3:=expand((1/24)*(2*x1+x2+x4)^2*(4*x1+6*x5-x2+6*x3-x4));

> u3:=[a,b,c];

> M1:=transpose(array([v1,v2,v3,v4,v5,u3]));

> b213:=1; b143:=1; b423:=1/2; b125:=1; b245:=1/2; b415:=1;

Calculate b115 (which should equal 2). r:=[2,0,0,0,1]. F125:=125. F415:=415.

> F1251:=(-det(submatrix(M1,[1,2,3],[2,5,6])))^1;

> F1252:=(det(submatrix(M1,[1,2,3],[1,5,6])))^(-1);

> F1255:=(-det(submatrix(M1,[1,2,3],[1,2,6])))^0;

> F4154:=(-det(submatrix(M1,[1,2,3],[1,5,6])))^(-1);

> F4151:=(det(submatrix(M1,[1,2,3],[4,5,6])))^1;

> F4155:=(-det(submatrix(M1,[1,2,3],[4,1,6])))^0;

> b115:=b125*F1251*F1252*F1255+b415*F4154*F4151*F4155;

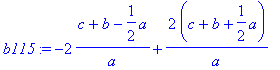
> expand(%);

Calculate b111 (which should equal 4). r:=[3,0,0,0,0]. F125:=125. F415:=415. F213:=213. F143:=143.

> F1251:=(-det(submatrix(M1,[1,2,3],[2,5,6])))^2;

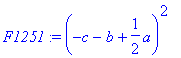
> F1252:=(det(submatrix(M1,[1,2,3],[1,5,6])))^(-1);

> F1255:=(-det(submatrix(M1,[1,2,3],[1,2,6])))^(-1);

> F4154:=(-det(submatrix(M1,[1,2,3],[1,5,6])))^(-1);

> F4151:=(det(submatrix(M1,[1,2,3],[4,5,6])))^2;

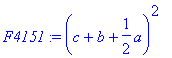
> F4155:=(-det(submatrix(M1,[1,2,3],[4,1,6])))^(-1);

> F2132:=(-det(submatrix(M1,[1,2,3],[1,3,6])))^(-1);

> F2131:=(det(submatrix(M1,[1,2,3],[2,3,6])))^2;

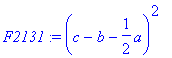
> F2133:=(-det(submatrix(M1,[1,2,3],[2,1,6])))^(-1);

> F1431:=(-det(submatrix(M1,[1,2,3],[4,3,6])))^2;

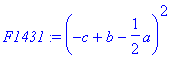
> F1434:=(det(submatrix(M1,[1,2,3],[1,3,6])))^(-1);

> F1433:=(-det(submatrix(M1,[1,2,3],[1,4,6])))^(-1);

> b111:=b125*F1251*F1252*F1255+ b415*F4154*F4151*F4155+ b213*F2132*F2131*F2133+ b143*F1431*F1434*F1433;

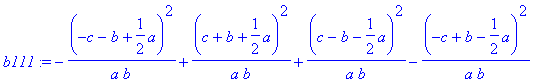
> expand(%);

>