A Very Short List of Examples of Maple commands

Maple can be used to do many-digit arithmetic

Exponentiation

>

2^100;

Factorials

>

100!;

Roots

>

sqrt(2);

Floating point evaluation to specified number of digits

>	evalf(sqrt(2),25);

Maple can work with algebraic expressions

Multiplying polynomials

>	expand((3-4*x)^5);

Factoring polynomials

>	factor(x^100-1);

Solving equations (including the complex solutions)

>	solve(x^3=8);

>	solve(a*x^2+b*x+c=0,x);

Simplifying expressions

>	(x^2-4)/(x-2);

>	simplify((x^2-4)/(x-2));

Maple can plot functions

Functions of one variable

>	plot(sin(x)+cos(x/2), x=-10..10);

Functions of two variables.  After plotting, you can click and rotate it.

>	plot3d(x^2+y^3,x=-2..2,y=-2..2);

Maple can carry out calculus computations

>	diff(x^10+sin(x)+sec(x),x);

>	integrate(x^10+sin(x)+sec(x),x);

>	integrate(x^3,x=0..3);

Maple can work with matrices

>	with(LinearAlgebra):

>	A:=Matrix([[1,2,3],[4,5,6]]);

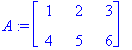
>	B:=Matrix([[7,8],[9,10],[11,12]]);

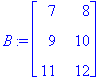
>	Multiply(A,B);

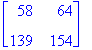
Rotation matrix for 30 degrees

>	Matrix([[cos(30*Pi/180),-sin(30*Pi/180)],[sin(30*Pi/180),cos(30*Pi/180)]]);

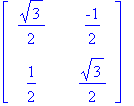
>	A:=Matrix(4,3,symbol=M);

>	B:=Matrix(3,2,symbol=N);

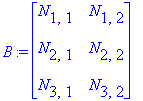
>	Multiply(A,B);

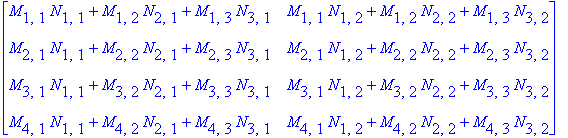
Maple can plot polyhedra.  After plotting you can click and rotate it.

>	with(plots):

>	p1:=[1,1,0]; p2:=[-1,1,0]; p3:=[-1,-1,0]; p4:=[1,-1,0]; p5:=[0,0,5];

>	polygonplot3d([[p1,p2,p3,p4],[p1,p2,p5],[p2,p3,p5],[p3,p4,p5],[p4,p1,p5]],scaling=constrained);

>