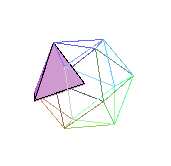
Tetrahedron B
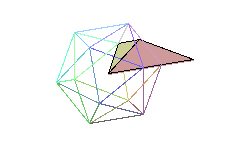
by Aaron Zerhusen
University of Kentucky
Lexington, Kentucky 40506
May 1997
Revised August 1997
email: abzerh00@sac.uky.edu
Copyright (C) 1997. Permission is granted to anyone to make or distribute copies of this document, in any medium, provided that the copyright notice and permission notice are preserved, and that the distributor grants the recipient permission for further redistribution as permitted by this notice.
The best place to begin exploring the world of aperiodic tilings is with an understanding of translations. A tiling has translational symmetry if the tiling can be shifted by a given distance in a given direction (think vector addition) such that it exactly matches itself. Now that we've covered what a translation is we can define some necessary terms. These definitions are taken from Marjorie Senechal's book Quasicrystals and Geometry.
Let A be a tiling of En, where En is n-dimensional space with the Euclidean metric. Then A is periodic if it admits translations in n linearly independent directions. Examples of periodic tilings are very common. Bathroom tiles, bricks in a wall, and several others are around us constantly.
Therefore it makes sense to call a tiling which admits no translations nonperiodic. n-dimensional tilings that admit translations in at most k linearly independent directions, where 0<k<n are called subperiodic by Senechal.
If a given set of tiles will only tile in a nonperiodic way, this set is called aperiodic. An aperiodic tiling is a tiling by an aperiodic set of tiles. Obviously, every aperiodic tiling is nonperiodic, but not every nonperiodic tiling is aperiodic.
For examples of aperiodic tilings, see the Quasitiler site. The program will generate a variety of tilings using higher dimensional lattices.
As one might assume from this definition, there are sets of tiles which will only tile in a nonperiodic way, and some which tile both periodically and nonperiodically, such as the set consisting of the single isosceles triangle whose interior angles measure 30°, 75°, and 75°. This triangle will tile periodically, or in a spiral nonperiodic form.
The most famous example of an aperiodic set of tiles is the pair of Penrose tiles, known as the kite and the dart. There is no known set consisting of a single tile which is aperiodic under this definition, although there is a known three-dimensional tile whose tilings have only two directions of translational symmetry. These aperiodic tiles have unique properties which make them distinct from other tiles. Some aperiodic tilings possess apparent five- or seven-fold rotational symmetries, which are not allowed in classical crystallography. In addition, some aperiodic tilings have unique inflations and deflations. This can best be described by example, and I will explain in detail the inflation and deflation rules for a set of three-dimensional analogues to Penrose's tiles by Danzer.
L. Danzer has developed a set of four tetrahedral prototiles which, by following a simple set of matching rules, tile space aperiodically. These tiles were introduced in a paper entitled "Three-Dimensional Analogs of the Planar Penrose Tilings and Quasicrystals". These make an excellent introduction to aperiodic tilings since they can be modelled using the Zometool kit, and the properties of inflation and deflation can easily be seen from the models.
Tetrahedron A Tetrahedron B
Tetrahedron C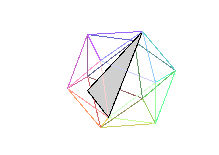
Tetrahedron K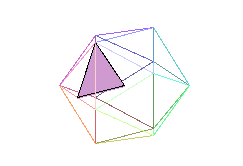
The lines which compose the tetrahedra are grouped into three classes, which Danzer calls red, white, and green. All of the edges have lengths which are multiples of the golden ratio, which will be designated by the Greek letter tau. The lengths are as follows:
| red | taun |
| white | a*taun, a=cos18° |
| green | b*taun, b=cos30° |
Then, by labelling the tetrahedra A, B, C, and K and the vertices 1, 2, 3, and 4, instructions to create the tetrahedra can easily be given, using the table of edge lengths which Danzer provides.
| tetrahedron | ||||||
| 1-2 | 2-3 | 3-1 | 2-4 | 1-4 | 3-4 | |
| A | a | b*tau | a*tau | a | 1 | b |
| B | a | a*tau | b*tau | b | a*tau-1 | 1 |
| C | a*tau-1 | b*tau | tau | b | a | a |
| K | a | b | a*tau-1 | tau/2 | 1/2 | (tau-1)/2 |
First we must establish which Zometool pieces correspond to Danzer's colored edges. In the Zometool kit, the blue pieces have lengths of taun, red are a*taun, and yellow are b*taun. However, since the K tetrahedron uses lengths which are 1/2 as long as the others, two Zometool pieces must be joined together for most of the edges. To simplify matters, here is a table of which Zometool pieces to use for the tetrahedron lengths as Danzer describes them on page 4 of his paper.
| edge length | Zometool pieces | Danzer's color |
| tau-1 | two short blue | red |
| 1 | two medium blue | |
| tau | two long blue | |
| a*tau-1 | two short red | white |
| a | two medium red | |
| a*tau | two long red | |
| b*tau-1 | two short yellow | green |
| b | two medium yellow | |
| b*tau | two long yellow |
To construct the tetrahedra I recommend first constructing the triangle of the 1, 2, and 3 vertices and then connecting the remaining three edges to the fourth vertex. For example, to make tetrahedron A make a triangle with sides of length a, tau*b, and tau*a. Then at vertex 1, where a and a*tau connect, add edge 1-4, which has length 1. Repeat this for the other vertices, 2 and 3. There will be only one configuration which allows all of the edges to meet at the proper vertices.
These may sound a little confusing at first, but just make a few models and hold them up against each other, and all will be made clear. Two tiles with mirror image faces may be matched up along those faces, unless the matched faces contain a blue (Zometool color) edge, in which case there is an additional restriction that the tiles themselves must be mirror images of each other. This latter restriction forces the tetrahedra to form octahedra of a single type of tile. Tiles A, B, and C form octahedra of four tiles. Tile K forms an octahedron of eight tiles. Of these four octahedra, two are concave and look like three-dimensional versions of Penrose's darts, and the other two are convex and resemble the kites.
Many aperiodic sets of tiles can be inflated, that is, a tile can be presented as a union of tiles smaller by a given factor, in this case a factor of tau. Danzer's tiles exhibit this property, and the inflation preserves the matching rules. By inflating, then increasing the size of the resulting smaller tiles by tau, and repeating, an infinite tiling can be created.
Using Zometool, models of tiles can be made following these rules which are, as I previously noted, tau larger then their components. Here are instructions for composing these infation tiles. I use the notation 1K to designate vertex 1 of the K tetrahedron.
This requires one K and one B model.
Attach the 123 face of K to the 124 face of B such that 1K meets
1B,
2K meets 2B, and 3K meets 4B.
This requires three B, two C, and six K models.
Attach two B's along the 134 face. Attach four K's around the medium
blue
(length one) edge. The K construction will fit inside the concave
region
of the B construction and be attached here. Place this in front of
you
with the K's toward you and the blue edges flat against the table.
Attach
another B to the B on your right along the 123 face. Connect two K's
on
the 124 face. Attach that to the 124 face of the B you just added.
There
should now be a convex pocket on your right formed by K's. Connect the
remaining two C's along face 134. They will fit in this pocket.
This requires two B, one C, and four K models.
Attach the two B's along the 134 face. Attach the four K's around the
medium
blue edge and as before the K construction fits in the concave pocket.
Attach the 124 face of the C to the 123 face of one of the K's.
This requires one A, two C, and two K models.
Connect the two K's on the 134 face. Attach the 124 face of a C to
the
123 face of one of the K's. Attach the second C to the other C along the
134
face. To the exposed 124 face of the second C attach the 234 face of the
A.
For some of the models I didn't specify which side of a symmetrical construction to attach a tile. This is because it doesn't matter in those cases; picking a different side will result in a mirror image. Notice that the lengths of the inflations utilize the fact that tau^2=tau+1.
Danzer, L. "Three-Dimensional Analogs of the Planar Penrose Tilings and Quasicrystals." Discrete Mathematics 76 (1989):1-7.
Zometool is a construction kit consisting of balls and struts, especially suitable for building structures having angles associated with dodecahedra and icosahedra. Further information on ordering can be obtained by contacting Zometool Marketing, 1526 South Pearl Street, Denver, CO 80210, 888-966-3386, sales@zometool.com, or visiting their website http://www.zometool.com/.