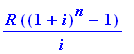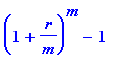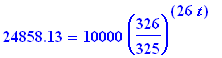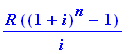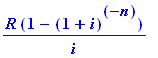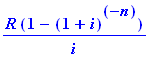Homework C1 like problems
Q.1.
If you invest $1,678.89 at 7% simple interest, how much will your investment be worth in 14 months?
Given: P,r,t find A for simple interest.
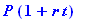
| > |
asval(1678.89,7/100,14/12);
|

Q.2.
If you invest $300
per month
at 4.40%
compounded monthly
, how much will your investment be worth in 25 years?
Given: R,r,t. Find S.
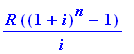
| > |
sval(300,4.4/1200,25*12);
|
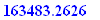
Q.3.
A company contributes $190 per month into a retirement fund paying 4.10% compounded monthly and employees are permitted to invest up to $ 2,200 per year into another retirement fund which pays 4.10% compounded annually.
How large can the combined retirement fund be worth in 25 years?
Given two annuities with different terms.
| > |
ans1:=sval(190,4.1/1200,25*12);
|
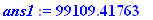
| > |
ans2:=sval(2200,4.1/100,25);
|

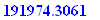
Q.4.
How much did you invest
each month
at 6%
compounded monthly
if 20 years later the investment is worth $184,816.36?
| > |
184816.36 = sval(R,6/1200,20*12.0);
|
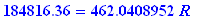
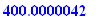
Q.5.
If you invest $762.40 and after 17 months it is worth $838.00, what
simple interest rate,
expressed as a percentage and rounded to .01, did you receive?
| > |
838.00=asval(762.4,r,17/12);
|
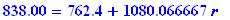

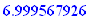
Q.6.
If you invest $8,000 at 7% compounded monthly, how much will your investment be worth in 7 years?
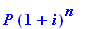
| > |
aval(8000.00,7/1200,7*12);
|
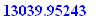
Q.7.
If you invest $2,111.70 at 9% simple interest, after how many months, rounded to .01, will your investment be worth $2,278?
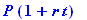
| > |
2278=asval(2111.70,9/100,t/12);
|

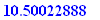
Q.8.
Homer won a prize in the lottery of $3,000, payable $1,500 immediately and $1,500 plus 6% simple interest payable in 260 days. Getting impatient, Homer sells the promissory note to Moe for $1,450 cash after 150 days. Using a nominal 360 day year, find the simple interest rate, rounded to .01, earned by Moe.
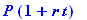
| > |
asval(1500,6/100,260/360);##Homer's expected earning at full term.
##This is also Moe's final payoff.
##Moe's investment is 1450 for 260-150=110 days.
|

| > |
1565=asval(1450,r,110/360);
|
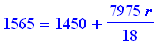

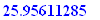
Q.9.
How much did you invest at 8% compounded bi-weekly if 15 years later the investment is worth $64,000?
Answer: ok dollars
.
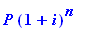
| > |
64000=aval(P,8.0/2600,15*26);
|
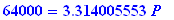
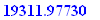
Q.10.
Bank A is offering an interest rate of 6.40% compounded monthly, while bank B is offering an interest rate of 6.42% compounded bi-weekly.
The effective rate offered by bank A = ok %,
while the effective rate offered by bank B = %.
For the investor, the bettter rate is being offered by bank
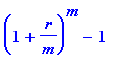
| > |
rate1:=reff(6.4/100,12);100*%;
|
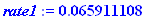
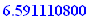
| > |
rate2:=reff(6.42/100,26);100*%;
|
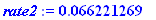
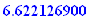
Q.11.
If you finance $50,000 of the purchase of your new home at 4.20% compounded monthly for 30 years, the monthly payment will be $244.51. If instead your had a rate of 5.10% compounded monthly for 15 years, the monthly payment will be $398.01. How much do you pay in total for the $50,000 mortgage if you finance it for 30 years?
Total payment =
How much do you save (in total payments) if you finance for 15 years instead?
No special formulas are involved. You are just computing total payments (or payouts).
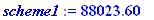
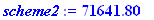
| > |
saving:=scheme1-scheme2;
|
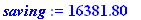
Q.12
How much did you invest at 5% simple interest if 13 months later the investment is worth $2,594?
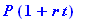
| > |
2594.0=asval(P,5/100,13/12);
|
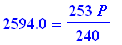
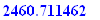
Q.13.
If you invest $10,000 at 8% compounded bi-weekly, after how many years, rounded to .01, will your investment be worth $24,858.13?
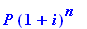
| > |
24858.13=aval(10000,8/2600,26*t);
|
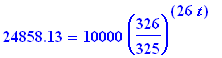

Homework C2 like problems
Q.1.
You plan on buying equipment worth 16,000 dollars in 3 years. Since you firmly believe in not borrowing, you plan on making monthly payments into an account that pays 5.40% compounded monthly . How much must your payment be?
Use the future value formula for annuity.
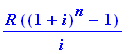
| > |
16000=sval(R,5.4/1200,3*12);
|
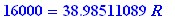
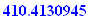
Q.2. If you finance $94,000 of the purchase of your new home at 4.40% compounded monthly for 14 years, how much would the monthly payment be?
You have an annuity with given present value. Find R.
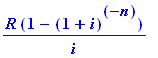
| > |
94000=pval(R,4.4/1200,14*12);
|
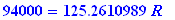

Q.3. If you can afford a monthly payment of $1050 for 33 years and if the available
interest rate is 6.00%, what is the maximum amount that you can afford to borrow?
You are looking for the present value given R,r,t.
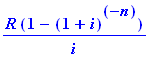
| > |
pval(1050,6.0/1200,33*12);
|
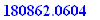
Q.5.
You plan on taking a 4 year hiatus to relax. If you plan on making monthly withdrawals of $1,900 from a money market account that pays 4.20% compounded monthly to finance your inactivity, how much must you invest at the outset to be able to afford this?
Again we need the present value of a 4 year annuity.
| > |
pval(1900,4.2/1200,4*12);
|
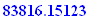
Just for comparison, calculate how much total money you will actually withdraw. The answer is 1900*12*4=91200.
Thus you collect
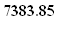 $ more than what you invest, because of the accumulated interest.
$ more than what you invest, because of the accumulated interest.
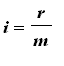 can be called the periodic interest rate
can be called the periodic interest rate
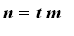 number of periods (instead of years)
number of periods (instead of years)