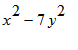
The Brouncker algorithm for the continued fractions of a root of a quadratic.
| > | with(linalg): |
To start, we create a matrix from
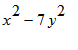
| > | A:=matrix(2,4,[1,0,1,0,0,1,0,-7]); |
| > |
![A := matrix([[1, 0, 1, 0], [0, 1, 0, -7]])](images/confrac_brouncker2.gif)
The function "fun" produces a polynomial in x,y from a 2 x 2 matrix. We need its values to calculate steps.
| > |
| > | fun:=m-> unapply(m[1,3]*x^2+2*m[1,4]*x*y+m[2,4]*y^2,x,y); |
![]()
| > | fun(A)(x,y);fun(A)(3,1); |
![]()
![]()
The function ch(m,t,n) changes matrix m as follows:
If n=1 then it add t times row 1 to row 2.
If n=2 it adds t times row 2 to row 1.
Then it makes a symmetric matrix operation on the last two columns.
| > | ch:=proc(m,t,n) local tmp: tmp:=copy(m); if n=1 then tmp:=addrow(tmp,1,2,t); tmp:=addcol(tmp,3,4,t); elif n=2 then tmp:=addrow(tmp,2,1,t);tmp:=addcol(tmp,4,3,t);fi;op(tmp);end: |
| > |
We start work on
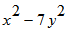 .
.
We shall record the t-values as we proceed.
| > | A:=matrix(2,4,[1,0,1,0,0,1,0,-7]); |
![A := matrix([[1, 0, 1, 0], [0, 1, 0, -7]])](images/confrac_brouncker7.gif)
We check the function at (1,1);
If it is less than 1, then we try values at (t,1) and stop just before the values change sign.
| > | fun(A)(1,1); fun(A)(2,1);fun(A)(3,1); |
![]()
![]()
![]()
So set t=2 and n=1(because the value at (1,1) was less than 1.)
| > | tvals:=[2]; |
![]()
| > | A1:=ch(A,2,1); |
![A1 := matrix([[1, 0, 1, 2], [2, 1, 2, -3]])](images/confrac_brouncker12.gif)
Repeat with new matrix. Here, the value at (1,1) is bigger than 1 , so we try (1,t), until sign changes.
| > | fun(A1)(1,1);fun(A1)(1,2); |
![]()
![]()
So we set t=1 and n=2 (because the value at (1,1) was bigger than 1.)
| > | tvals:=[op(tvals),1]; |
![]()
| > | A2:=ch(A1,1,2); |
![A2 := matrix([[3, 1, 2, -1], [2, 1, -1, -3]])](images/confrac_brouncker16.gif)
Repeat! Again, we get t=1, n=1.
| > | fun(A2)(1,1);fun(A2)(2,1); |
![]()
![]()
| > | tvals:=[op(tvals),1]; |
![]()
| > | A3:=ch(A2,1,1); |
![A3 := matrix([[3, 1, 2, 1], [5, 2, 1, -3]])](images/confrac_brouncker20.gif)
This is special!
We have the f(1,1) value exactly equal to 1 . In this case, we set t=1 and n equal to the opposite of before, so n=2.
| > | fun(A3)(1,1); |
![]()
| > | tvals:=[op(tvals),1]; |
![]()
| > | A4:=ch(A3,1,2); |
![A4 := matrix([[8, 3, 1, -2], [5, 2, -2, -3]])](images/confrac_brouncker23.gif)
| > | fun(A4)(1,1);fun(A4)(2,1);fun(A4)(3,1);fun(A4)(4,1);fun(A4)(5,1); |
![]()
![]()
![]()
![]()
![]()
Now we get t=4, n=1.
| > | tvals:=[op(tvals),4]; |
![]()
| > | A5:=ch(A4,4,1); |
![A5 := matrix([[8, 3, 1, 2], [37, 14, 2, -3]])](images/confrac_brouncker30.gif)
| > | seq(cat(A,i)=op(cat(A,i)),i=1..5); |
![A1 = matrix([[1, 0, 1, 2], [2, 1, 2, -3]]), A2 = matrix([[3, 1, 2, -1], [2, 1, -1, -3]]), A3 = matrix([[3, 1, 2, 1], [5, 2, 1, -3]]), A4 = matrix([[8, 3, 1, -2], [5, 2, -2, -3]]), A5 = matrix([[8, 3, 1...](images/confrac_brouncker31.gif)
Note that A1 and A4 have a repeat of the second part . So, now the pattern repeats!
| > | convert(sqrt(7), confrac,8,ans7); |
![]()
| > | ans7; |
![]()
| > |
Case of
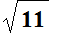
| > |
Case of
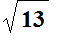
Now try yet another,
![]()
| > | A:=matrix(2,4,[1,0,1,0,0,1,0,-13]);tvals:=[]; |
![A := matrix([[1, 0, 1, 0], [0, 1, 0, -13]])](images/confrac_brouncker61.gif)
![]()
| > | fun(A)(1,1); |
![]()
| > | seq([t,fun(A)(t,1)],t=1..5); |
![]()
| > | tvals:=[op(tvals),3]; |
![]()
| > | A1:=ch(A,3,1); |
![A1 := matrix([[1, 0, 1, 3], [3, 1, 3, -4]])](images/confrac_brouncker66.gif)
| > | fun(A1)(1,1); |
![]()
| > | seq([t,fun(A1)(1,t)],t=1..5); |
![]()
| > | tvals:=[op(tvals),1];A2:=ch(A1,1,2); |
![]()
![A2 := matrix([[4, 1, 3, -1], [3, 1, -1, -4]])](images/confrac_brouncker70.gif)
| > | fun(A2)(1,1); |
![]()
| > | seq([t,fun(A2)(t,1)],t=1..8); |
![]()
| > | tvals:=[op(tvals),1];A3:=ch(A2,1,1); |
![]()
![A3 := matrix([[4, 1, 3, 2], [7, 2, 2, -3]])](images/confrac_brouncker74.gif)
| > | fun(A3)(1,1); |
![]()
| > | seq([t,fun(A3)(1,t)],t=1..8); |
![]()
| > | tvals:=[op(tvals),1];A4:=ch(A3,1,2); |
![]()
![A4 := matrix([[11, 3, 4, -1], [7, 2, -1, -3]])](images/confrac_brouncker78.gif)
| > | fun(A4)(1,1); |
![]()
| > | seq([t,fun(A4)(t,1)],t=1..8); |
![]()
| > | tvals:=[op(tvals),1];A5:=ch(A4,1,1); |
![]()
![A5 := matrix([[11, 3, 4, 3], [18, 5, 3, -1]])](images/confrac_brouncker82.gif)
| > | fun(A5)(1,1); |
![]()
| > | seq([t,fun(A5)(1,t)],t=1..8); |
![]()
| > | tvals:=[op(tvals),6];A6:=ch(A5,6,2); |
![]()
![A6 := matrix([[119, 33, 4, -3], [18, 5, -3, -1]])](images/confrac_brouncker86.gif)
| > | fun(A6)(1,1); |
![]()
| > | seq([t,fun(A6)(t,1)],t=1..8); |
![]()
| > | tvals:=[op(tvals),1];A7:=ch(A6,1,1); |
![]()
![A7 := matrix([[119, 33, 4, 1], [137, 38, 1, -3]])](images/confrac_brouncker90.gif)
| > | fun(A7)(1,1); |
| > | seq([t,fun(A7)(1,t)],t=1..8); |
![]()
![]()
| > | tvals:=[op(tvals),1];A8:=ch(A7,1,2); |
![]()
![A8 := matrix([[256, 71, 3, -2], [137, 38, -2, -3]])](images/confrac_brouncker94.gif)
| > | fun(A8)(1,1); |
![]()
| > | seq([t,fun(A8)(t,1)],t=1..8); |
![]()
| > | tvals:=[op(tvals),1];A9:=ch(A8,1,1); |
![]()
![A9 := matrix([[256, 71, 3, 1], [393, 109, 1, -4]])](images/confrac_brouncker98.gif)
| > | fun(A9)(1,1);## Special Case |
![]()
| > | tvals:=[op(tvals),1];A10:=ch(A9,1,2); |
![]()
![A10 := matrix([[649, 180, 1, -3], [393, 109, -3, -4]])](images/confrac_brouncker101.gif)
| > | fun(A10)(1,1); |
![]()
| > | seq([t,fun(A10)(t,1)],t=1..8); |
![]()
| > |
| > | tvals:=[op(tvals),6];A11:=ch(A10,6,1); |
![]()
![A11 := matrix([[649, 180, 1, 3], [4287, 1189, 3, -4]])](images/confrac_brouncker105.gif)
| > | seq(cat(A,i)=op(cat(A,i)),i=1..11); |
![A1 = matrix([[1, 0, 1, 3], [3, 1, 3, -4]]), A2 = matrix([[4, 1, 3, -1], [3, 1, -1, -4]]), A3 = matrix([[4, 1, 3, 2], [7, 2, 2, -3]]), A4 = matrix([[11, 3, 4, -1], [7, 2, -1, -3]]), A5 = matrix([[11, 3,...](images/confrac_brouncker106.gif)
![A1 = matrix([[1, 0, 1, 3], [3, 1, 3, -4]]), A2 = matrix([[4, 1, 3, -1], [3, 1, -1, -4]]), A3 = matrix([[4, 1, 3, 2], [7, 2, 2, -3]]), A4 = matrix([[11, 3, 4, -1], [7, 2, -1, -3]]), A5 = matrix([[11, 3,...](images/confrac_brouncker107.gif)
Note that A11 has same second part as A1. So, now we repeat.
![]()
| > | unassign('ans13');convert(sqrt(13),confrac,15,ans13); |
![]()
| > | ans13; |
![]()
| > |
| > |
| > |