Drawing diagrams to accompany problems.
You can often think of a picture or diagram that would be useful in the statement of a problem. We can use Maple to draw these pictures, using words from plots and plottools, packages of words used to draw pictures, and also from MCtools, which is the same package that contains tagit, and should be loaded at the beginning of each session. To see the words in a package and at the same time make them usable, load the package using with
| > | with(plots); with(plottools); with(MCtools); |
There are a lot of words here, but just like the regular vocabulary, the words in plots and plottools all have help pages too. The MCtools package does not have help pages, but the command mctools() does provide some basic online help. The main drawing words in MCtools are DL , DV , GP , PA , PC , and PT . These were designed to give easy access to some of the words in plots and plottools.
One of the words you will use a lot is display from the plots package. You draw different parts of the picture you are thinking of and give them names, then you display them together.
When you have a picture to draw, you can always load plots and plottools and scan for words which might help you make the drawing. You can bring up the help sheet on words that might help you and look at the examples there. There is also an extensive drawing tutorial you can consult later in this text.
| > |
Problem: Draw a floor plan for a rectangular kitchen which is 10 by 20 and has a 2 by 4 sink along the long side.
Solution : We use plots[polygonplot] to draw the floor. The floor is a rectangle, so we set up a coordinate system and assign coordinates to the vertices of the rectangle.
| > | fl := [[0,0],[20,0],[20,10],[0,10],[0,0]]; |
![]()
Now draw the floor with polygonplot and color it yellow. Give a name to the drawing.
| > | pl1:=plots[polygonplot](fl,color=yellow); |
![]()
Now draw a sink and give it a name.
| > | sink := [[8,0],[12,0],[12,2],[8,2],[8,0]]; |
| > | pl2:= plots[polygonplot](sink,color=magenta); |
![]()
![]()
We display both of these pictures together using display from the plots package. We use the option scaling = constrained because we want the same scale on both axes.
| > | plots[display](pl2,pl1,scaling=constrained); |
![[Maple Plot]](images/parameterize5.gif)
Other solutions: We could have used polygon from the plottools package to draw the floor and sink.
| > |
We might want to label the diagram. This can be done with plots[textplot] or more easily with PT (put text) from the MCtools package. The labels can be created created and named separately and added to the display or they can simply be put into the display as below.
| > | plots[display](PT([7,1],2),pl2,pl1,scaling=constrained); |
![[Maple Plot]](images/parameterize6.gif)
After you get all the labels added you can remove the axes by adding the option axes = none.
| > | plots[display](PT([7,1],2),pl2,pl1,scaling=constrained,axes=none); |
Note: The process of naming the parts to a drawing and displaying them together can be carried out several ways. A good way is to develop the drawing in a single input cell, using the shift return to add new lines to the input cell. Our drawing could have been developed like so:
| > | fl := [[0,0],[20,0],[20,10],[0,10],[0,0]]: pl1:=polygonplot(fl,color=yellow): sink := [[8,0],[12,0],[12,2],[8,2],[8,0]]: pl2:= plots[polygonplot](sink,color=magenta): plots[display](PT([7,1],2),pl2,pl1,scaling=constrained); |
| > |
We can make up a problem which uses this diagram.
QM_[0;200-6;four]
A kitchen floor which is 10 feet by 20 feet is to be tiled, except for a 2 foot by 3 foot cabinet along one of the long walls (see the diagram).
![[Maple Plot]](images/parameterize7.gif)
If we use tiles which are 12 inches square, how many tiles will be needed?
AC_[4]
AH_[0]
If we use tiles which are 6 inches square, we will need
AS_[two,three,four]
times as many tiles.
SKIP_
| > |
Problem.
Make up and solve an area problem about a polygon such as a rectangle with some cutouts, or a trapezoid. Draw a diagram for the statement of the problem and add the problem with accompanying diagram to your WHS homework.
Problem.
Duplicate this drawing.
![[Maple Plot]](images/parameterize8.gif)
I will get you started: plots[display](
Another example: Draw an ice cream cone
A solution. There might be some words in the plottools package to help here.
| > | with(plottools); |
Yes. cone and sphere are the words we are looking for. What is their syntax? we can type
| > | example(cone); |
This brings up the helpsheet for cone and goes to the examples section. copy the example and paste it into your worksheet. Then bring up the helpsheet for sphere. (Actually that word is used in other packages in Maple, so you have to choose. Or you can say example(plottools[sphere]); )
Here is diagram we have developed from the helpsheets.
| > | icecream := cone([0,0,-1],0.7,color=yellow),sphere([0,0,0.1],0.6,color=pink): plots[display](icecream, scaling=constrained, style=patch,axes=boxed); |
This does not solve our problem. We want the sides of the cone to be tangent to the sphere.
It is easier to see in cross section. The angle drawn from the center of the sphere [0,0,z] to the point of tangency [.7,0,0] and then to the base of the cone [0,0,-1] should be a right triangle. So
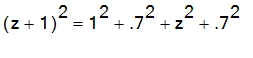 . Solving for z, we get z = .7^2. So the radius of the sphere is
. Solving for z, we get z = .7^2. So the radius of the sphere is
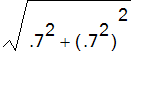 = .854 approximately
= .854 approximately
| > |
So we can modify the drawing to solve the problem.
| > | icecream := plottools[cone]([0,0,-1],.7,color=yellow), plottools[sphere]([0,0,.7^2],.854,color=pink): plots[display](icecream, scaling=constrained); |
We can label this diagram using the MCtools word PT. Note we have also changed the rendering of the ice cream by changing the style and lightmodel.
| > | plots[display](PT([0,0,1.5],`cone radius = 3.5 inches`,color=red),icecream,scaling=constrained,style=patchnogrid,lightmodel=light4); |
| > |
Note the use of the word plots[display]. This is used to display several plots in the same picture. By using it as plots[display] instead of in the form display, it is not necessary to have loaded the plots package into vocabulary in order to use it. (If you say display(icecream) and have not loaded the plots package by saying with(plots) first, the output will be the input 'display(icecream)'.)
Often a problem is easier to understand if it is accompanied by an appropriate diagram. Or perhaps the diagram may serve only to focus attention on the problem, and make it more interesting. In this case, we also are drawing the diagram to check our own solution to the problem.
Draw the diagram after a skip tag and before the qm tag, then copy and paste it into the problem
QM_[0;5*sqrt(.7^2 + (.7^2)^2)]
![[Maple Plot]](images/parameterize11.gif)
A cone has a a height of 5 inches, and a radius of 3.5 inches. What is the radius of the ice cream ball that just fits in the cone?
AC_[8]
SKIP_
Problem: Make a problem which has a three dimensional diagram in it. Solve the problem. Then post it to your WHS homework along with the diagram.
| > |
Here are the 24 named colors in Maple
| > | colors(); |
![[Maple Plot]](images/parameterize12.gif)
| > |
Custom color can be created with the plot option color=COLOR(RGB,r,g,b) where r, b, and g are numbers between 0 and 1. So COLOR(RGB,1,0,0) is red, COLOR(RGB,0,1,0) is green , and COLOR(RGB,0,0,1) is blue. Also COLOR(RGB,0,0,0) is black , and COLOR(RGB,1,1,1) is white. Other mixtures, produce other colors: for example, yellow is equal parts of green and blue. The word trycolor defined below allows you to experiment with different values for r, b, and g and compare the results with the named colors.
| > | trycolor:=proc(r,g,b) plots[display](colors(),plottools[rectangle]([-10,20],[160,40],color=COLOR(RGB,r,g,b))) end: |
For example, Maple green is too lime. A much better green for display purposes is obtained by making it darker. So COLOR(RGB,0,1/2,0) is what some would call hunter green or forest green.
| > | trycolor(0,1/2,0); |
![[Maple Plot]](images/parameterize13.gif)
After you find a color you like, you can give it a name (using the word macro) and use it like you would the 24 named colors. However, the name must be redefined each time you open up the worksheet, if you plan to use the color again.
| > | ?plot[options] |
| > | macro(darkgreen=COLOR(RGB,0,1/2,0)); |
![]()
| > | plots[display](plottools[disk]([0,0],1,color=darkgreen)); |
![[Maple Plot]](images/parameterize15.gif)
| > |
Parameterized problems - problem generators
It is useful for many purposes to have several versions of the same problem with only the numbers changed. The numbers we change are called the parameters of the problem. We can insert letters to stand in for the parameters, then use some algebra or some other mathematical methods to solve the problem in terms of the parameters. Usually, this gives us a formula for the solution as a function of the parameters. Then to solve a specific version of the problem, we just plug the specific values of the parameters into the formula.
We loosely refer to this process as parameterizing the problem . Sometimes, and this is something you can pass on to your students, it is as easy or even easier to solve a parameterized version of the problem as it is to solve the original problem. In any case, the technique can be used by teachers to make up lots of problems which are the same except the numbers are different, without going through the solution each time.
Example of a parameterization of a problem
Here is an old nugget, which has been used for generations to train student to set up equations to solve problems.
Original Problem . Bill is 1/2 his father's age. In 10 years, he will be 2/3's his father's age. How old is he now?
Solution. Let x be Bill's age, and y be his father's age. The first sentence says x = 1/2*y. The second sentence says x + 10 = 2/3*(y+10). So y = 2*x and x + 10 = 2/3*(2*x + 10) = 4/3*x + 20/3. Solving for x, 1/3*x = 10 - 20/3, or x = 30-20 = 10. Bill is 10 years old.
We can check the solution with Maple using solve :
| > | solve({x = 1/2*y,x + 10 = 2/3*(y+10)}); |
To parameterize this problem and make a problem generator , first we compose the original problem using the word tagit from the MCtools package. We have already seen that this word relieves you of the burden of inserting tags into the problem; it also makes it easier to parameterize a problem, as we shall see. Here is the tagitized original problem.
| > | tagit("Bill is 1/2 his father's age. In 10 years, he will be 2/3's his father's age. How old is he now?",_AC(10)): |
QM_[0.05;10]
AH_[0]
Bill is 1/2 his father's age. In 10 years, he will be 2/3's his father's age. How old is he now?
AC_[5]
SKIP_
| > |
To Parameterize the problem:
There are 4 numbers in the problem. We could parameterize all of them, but for starters, we could restrict ourselves to just parameterizing the 10. Just replace 10 by a suitable letter, say n, and resolve the problem in terms of n.
Parameterized Problem . Bill's 1/2 as old as his father. In n years, he will be 2/3's as old. How old is Bill now?
Solution. Let x be Bill's age, and y be his father's age. The first sentence says x = 1/2*y. The second sentence says x + n = 2/3*(y+n). So y = 2*x and x + n = 2/3*(2*x + n) = 4/3*x + 2/3*n. Solving for x, 1/3*x= 1/3*n, or x = n. Bill is n years old.
Now make a problem generator in the following fashion: Define a procedure, we have called it prob below, which has the parameter n as input. That is given in the first line of the procedure (the 'proc' line ) after the proc line comes the body of the procedure, which in this case is just a call to tagit. The procedure definition ends with an 'end' line .
In order to actually define the procedure, you must execute the input cell containing the definiton. This only needs to be done once in any given Maple session, unless you change the definition.
Then when we execute the procedure with specific values for the parameter, an instance or version of the problem is generated.
Compare the use of tagit below with its use above. In particular, note how the 10 was change to an ",n,". This is called breaking out the parameter . The parameter cannot be enclosed in double quotes so the string the 10 was in is broken into a sequence of two strings with the parameter in between. We enclosed the problem statement in a list so that the parameter value would be printed inline, rather than printed centered on a separate line.
| > | prob:= proc(n) #the proc line tagit(["Bill is 1/2 as old as his father. In ",n," years, he will be 2/3's as old. How old is Bill?"],_AC(n)) end; # the end line |
![]()
Now, to generate an instance of the problem, just make a call to the procedure defining the problem.
| > | prob(15); |
QM_[0.05;15]
AH_[0]
Bill is 1/2 as old as his father. In 15 years, he will be 2/3's as old. How old is Bill?
AC_[5]
SKIP_
| > |
The nice thing about this is once you have the problem defined, it is easy to gererate several versions of the problem.
| > | prob(20): |
QM_[0.05;20]
AH_[0]
Bill is 1/2 as old as his father. In 20 years, he will be 2/3's as old. How old is Bill?
AC_[5]
SKIP_
| > |
Problem: Replace the 1/2 in the problem by a parameter a and the 2/3 by a parameter b. Solve the resulting parameterized problem. Make a copy of the problem generator we have already, and modify it to problem generator with three paramers n, a, and b. Test your solution by posting two or three versions of the problem.
When you are putting in values for the parameters, a problem arises: What values of the parameters give a problem which 'makes sense'?
Even before you solve the problem in terms of the parameters, you can sometimes figure out this answer. For example, here we can see that a and b must be between 0 and 1, a must be less than b if n is postive, a must be = b if n is 0 and a must be greater than b if n is negative.
But even more interesting questions come up. For what values of the parameters does the problem not only make sense, but comes out nice.
Question: In the problem: 'Bill is a as old as his father. In n years, he will be b as old. How old is Bill?', for what positive integers n, and ratios a and b with 0< a < b < 1 is Bill's age a positive integer < 120?
| > |
Another example: A carry problem
Here is an addition problem. We want the student to enter the correct carrys.
Carry _ _ _
7 8 9
+ 6 8 3
-------
_ _ _ _
This is an example where we can put ATcross to good use. The output is suppressed because it is so busy. It looks better when posted.
| > | tagit(standards=["Can carry correctly."],"Complete the addition. Put in the correct carrys.", _ATcross([["Carry:",[1],[1],[1],""], ["","",7,8,9], ["","+",6,8,3], ["",[1],[[4,2,3,1]],[7],[2]] ],txtboxsize=2)); |
Now we want to make a problem generator from this. First, we define and test a procedure to select an element at random from a given list or set.
| > | randelt := proc(set) local f; f := rand(1..nops(set)); set[f()] end: |
| > | seq(randelt({3,jack,10}),i=1..10); |
![]()
That seems to work. Now to turn the tagit line into a problem generator, we copy it down and start parameterizing. If we replace all six digits in the two terms of the sum by parameters then we can express the digits of the answer and the digits of the carry's as shown in the diagram below.
Carry ch ct cu
a b c
+ d e f
-----------
ch h t u
So here is the problem generator. We make use of irem and iquo to get the digits of the answer and the carry's.
| > | carry := proc(a,b,c,d,e,f) local u,t,h,cu,ct,ch,randelt; randelt := proc(set) local f; f := rand(1..nops(set)); set[f()] end: u := irem(c+f,10): cu := iquo(c+f,10); t := irem(cu+b+e,10): ct := iquo(cu+b+e,10); h := irem(ct+a+d,10): ch := iquo(ct+a+d,10); tagit(standards="Can carry correctly.","Complete the addition. Put in the correct carrys, including 0.", _ATcross([["Carry:",[ch],[ct],[cu],""], ["","",a,b,c], ["","+",d,e,f], ["",[[ch,ch+randelt([-1,1,2])]],[[h,h+randelt([-1,1,2])]],[t],[u]] ],txtboxsize=2)); end: |
| > |
Now test the generator.
| > | carry(3,2,4,5,6,3); |
| > |
| > |
Make the parameters random: Writing parameterless problem generators
After you have worked with a problem generator for awhile, you can use the rand function to supply values for the parameters in the generator.
We can use the randelt function to turn carry into a parameterless problem generator .
| > | carry := proc() local u,t,h,cu,ct,ch,randelt,a,b,c,d,e,f; randelt := proc(set) local f; f := rand(1..nops(set)); set[f()] end: a := randelt([seq(i,i=1..9)]); b := randelt([seq(i,i=0..9)]); #nonleading digits can be 0. c := randelt([seq(i,i=0..9)]); d := randelt([seq(i,i=1..9)]); e := randelt([seq(i,i=0..9)]); f := randelt([seq(i,i=0..9)]); u := irem(c+f,10): cu := iquo(c+f,10); t := irem(cu+b+e,10): ct := iquo(cu+b+e,10); h := irem(ct+a+d,10): ch := iquo(ct+a+d,10); tagit(standards="Can carry correctly.","Complete the addition. Put in the correct carrys, including 0.", _ATcross([["Carry:",[ch],[ct],[cu],""], ["","",a,b,c], ["","+",d,e,f], ["",[ch],[[h,h+randelt([-1,1,2])]],[t],[u]] ],txtboxsize=2)); end: |
Now we would test it by simply executing
| > | carry(); |
Writing a problem generator for adding m n-digit numbers.
This could be done using matrices and vectors to store the data. We would use the linalg package. It has a word linalg[randmatrix] to generate random matrices.
| > | linalg[randmatrix](3,2,entries=rand(1..9)); |
![matrix([[7, 5], [5, 1], [5, 6]])](images/parameterize18.gif)
| > |
Here is one solution. The word map is used to check the problem, since the output from ATcross is so extemely ugly and hard to read. We have also inserted the standards= option in this problem.
| > |
| > |
| > | carryprob := proc(m,n) local A,sm,cr,hold,hnew,i,j; A := linalg[randmatrix](m,n,entries=rand(1..9)); sm := vector(n+1); cr := vector(n+1); hold:= 0; cr[n+1]:=hold: for i from 1 to n do sm[n-i+2] := irem(hold+add(A[j,n-i+1],j=1..m) ,10,'hold'); cr[n-i+1]:=hold; od; if hold=0 then sm[1]:= `` else sm[1]:= hold fi: print(map(evalm,[cr,A,sm])); |
| > | tagit(standards=["Can carry correctly."],"Complete the addition. Put in the correct carrys.", _ATcross([["Carry:",seq([cr[i]],i=1..n),""], seq(["","",seq(A[j,i],i=1..n)],j=1..m-1), ["","+",seq(A[m,i],i=1..n)], ["",sm[1],seq([sm[i]],i=2..n+1)] ],txtboxsize=2)); |
| > | end: |
| > |
To make a random problem for the student to add three 4-digit numbers, we would just execute
| > | carryprob(3,4); |
| > |
Note: Maintainence problems arise when using randomly generated values for a parameter.
An example of a parameterized problem with a diagram
If you have a diagram that you want to add to a parameterized problem, just give a name to the plot and insert it into the problem=. For example:
Problem The right triangle shown (not to scale) has height 4 and hypotenuse 6. What is its area? What is its perimeter?
![[Maple Plot]](images/parameterize19.gif)
Solution:
let x = base. then x^2 + 4^2 = 6^2, by Pythagoras. so x = sqrt(36-16) = sqrt(20). so the area is 1/2*4*sqrt(20)= 4*sqrt(5)
and the perimater is 4+6+x= 10+sqrt(20)
Note:
| > |
| > | pic :=plots[display](PT([-1,2],4),PT([4,3],6),plottools[polygon]([[0,0],[0,4],[8,0]],color=yellow),axes=none); |
![]()
![]()
![]()
| > |
To compose this with tagit,
| > | tagit(pic,"The right triangle shown (not to scale) has height 4 and hypotenuse 6. \nIts area is ", _AC(4*sqrt(5)),", and its perimeter is ",_AC(4+6+sqrt(20))); |
QM_[0.05;4*5^(1/2);10+2*5^(1/2)]
AH_[0]
![[Maple Plot]](images/parameterize23.gif)
The right triangle shown (not to scale) has height 4 and hypotenuse 6.
Its area is
AC_[5]
AH_[0]
, and its perimeter is
AC_[5]
SKIP_
| > |
Note: the diagrams are always too large for the problem, and must be rescaled. The bad news is that this must be done by hand; the good news is that it only has to be done once. If you need to change something in the tagit line, then when you execute it again, the diagram assumes its new shap.
To parameterize the right triangle problem, we could parameterize both numbers
Problem The right triangle shown has height a and hypotenuse b. What is its area?
![[Maple Plot]](images/parameterize24.gif)
Solution: let x = base. then x^2 + a^2 = b^2, by Pythagoras. So x = sqrt(b^2-a^2). So the area is 1/2*a*sqrt(b^2-a^2)
Now to compose this for Mathclass, we can add a proc line and an end line, then break out the parameters, and replace the answers by the formulas which give the answers in terms of the parameters. Note: I have put the definition of pic right in the problem generator . That reduces the change of losing the picture and makes it easier to parameterize if you decide to do it. (See below)
| > | prob:=proc(a,b) local pic; pic := plots[display](PT([-1,2],a),PT([4,3],b), plottools[polygon]([[0,0],[0,4],[8,0]],color=yellow),axes=none); tagit(pic,["The right triangle shown (not to scale) has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end; |
![]()
![]()
![]()
![]()
![]()
![]()
| > | prob(3,4); |
QM_[0.05;2*7^(1/2);3+5/2*7^(1/2)]
AH_[0]
![[Maple Plot]](images/parameterize31.gif)
The right triangle shown (not to scale) has height 3 and hypotenuse 4.
Its area is
AC_[5]
AH_[0]
, and its perimeter is
AC_[5]
SKIP_
| > |
Problem : Parameterize this problem with 3 parameters: 'A right triangle with legs 3 and 4 is sitting on its hypotenuse, so that the hypotenuse is its base. What then is its height?' Solve the parameterized problem. Make a problem generator. Then insert a diagram into the problem generator.
Problem: Take one of your favorite problems and parameterize it with at least 1 parameter. Make it a problem generator from that.
A parameter whose value does not affect the answer to the problem is called an inessential parameter . For example, if the problem is 'What is the slope of the line ax + b = y?', the answer to the problem, a, is independent of the value of b. I would call b an inessential parameter to this problem.
Here is another example of an inessential: In the problem, 'a can mow a yard in 3 hours and Jim can mow it in 5 hours. How long does it take them to mow it together?', the parameter a can take on the value 'Bill' or 'Sue' or any other name (including 'a') without changing the answer to the problem.
We can introduce inessential parameters into a problem to change the way the problem looks or is stated as a device for introducing variety in versioned homework.
For example, in the 'Bill and his father' problem above we could parameterize Bill's name. All you have to do is break out Bill from each string in which it occurs in the statement of the problem and put Bill in the inputs to the problem. It is not necessary to change Bill to a because 'Bill' can be used as a name for a parameter. Below is the old prob followed by the new prob. Note the changes.
| > | prob:= proc(n) #the proc line tagit(["Bill is 1/2 as old as his father. In ",n," years, he will be 2/3's as old. How old is Bill?"],_AC(n)) end; # the end line |
![]()
| > | prob:= proc(Bill,n) #the proc line tagit([Bill," is 1/2 as old as his father. In ",n," years, he will be 2/3's as old. How old is ",Bill,"?"],_AC(n)) end; # the end line |
![]()
![]()
| > | prob(Sam,5); |
QM_[0.05;5]
AH_[0]
Sam is 1/2 as old as his father. In 5 years, he will be 2/3's as old. How old is Sam?
AC_[5]
SKIP_
Another example: In the 'right triangle' problem above, the color of the (interior of the) triangle is yellow. We can parameterize this color by just inserting 'clr' as an input to prob. Then we must supply the color as input.
| > | prob:=proc(a,b) local pic; pic := plots[display](PT([-1,2],a),PT([4,3],b), plottools[polygon]([[0,0],[0,4],[8,0]],color=yellow),axes=none); tagit(pic,["The right triangle shown (not to scale) has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end: |
| > | prob:=proc(a,b,clr) local pic; pic := plots[display](PT([-1,2],a),PT([4,3],b), plottools[polygon]([[0,0],[0,4],[8,0]],color=clr),axes=none); tagit(pic,["The right triangle shown (not to scale) has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end: |
| > |
| > | prob(3,4,blue); |
QM_[0.05;2*7^(1/2);3+5/2*7^(1/2)]
AH_[0]
![[Maple Plot]](images/parameterize35.gif)
The right triangle shown (not to scale) has height 3 and hypotenuse 4.
Its area is
AC_[5]
AH_[0]
, and its perimeter is
AC_[5]
SKIP_
| > |
Problem: Are there any inessential parameters you can introduce into the favorite problem you parameterized above? If so, introduce one of them into the inputs for your prob and re-post.
Often the diagram that goes with a WHS
problem generator
is static, that is, it does not change when the inputs are changed. Or, as in the case of the right triangle problem, the labels on the legs were changed in the original problem generator, and then when we introduced the color of the triangle as an inessential parameter later, we can parameterize the diagram as it sits in the problem.
Sometimes it is convenient to parameterize a diagram outside a problem generator. Then we can make a call to the diagram function in the problem generator.
Example : In the right triangle problem, if we wanted to draw the triangle to scale, then we have to worry about placing the labels correctly and also what the vertices of the triangle are going to be.
We could work on this leaving pic as a local variable in prob, but a more convenient way is to extract pic from prob and make a procedure out of it.
First how will we express the coordinates of the triangle in terms of a and b?
Keep one vertex at [0,0], and one of the others [0,a]. Now since b is the length of the hypotenuse, the vertex [x,0] on the x-axis satisfies
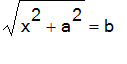 Solving for x, we get
Solving for x, we get
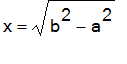 .
.
Next where will be place the labels in terms of a and b? A good place for the label of the vertical leg is at [-1,a/2], in other words, halfway up and to the left. Of course if a is very small, then the label will be way off to the left. A better place would be [-eps,a/2], where we make eps an 'adjustment' parameter to the diagram generator.
Now, where to place the label for the hypotenuse. How about just above and to the right of the midpoint of the hypotenuse? The midpoint is [sqrt(b^2-a^)/2,a/2], so we use our adjustment parameter. [sqrt(b^2-a^2)/2+eps,a/2+eps].
The diagram generator could look like this. Note that we have added the option scaling = constrained, since we have gone to the trouble of making a scaled diagram.
| > | pic := proc(a,b,clr,eps) plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr),axes=none,scaling=constrained); end: |
| > | pic(3,8,blue,.4); |
![[Maple Plot]](images/parameterize38.gif)
Now the problem generator has to be changed to incorporate the paramterized diagram. Note that we have modified the statement of the problem by taking out the disclaimer that the diagram is not to scale.
| > | prob:=proc(a,b,clr,eps) tagit(pic(a,b,clr,eps),["The right triangle shown has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end: |
| > |
Now test this.
| > | prob(3,7,pink,.3); |
QM_[0.05;4*10^(1/2);3+5*10^(1/2)]
AH_[0]
![[Maple Plot]](images/parameterize39.gif)
The right triangle shown has height 3 and hypotenuse 7.
Its area is
AC_[5]
AH_[0]
, and its perimeter is
AC_[5]
SKIP_
| > |
| > |
Optional Parameters: Inserting your own options into a diagram or problem generator
One of the things that happens after you learn to build generator is that the number of parameters in a procedure gets too long. It becomes difficult to remember the exact order of the parameters in the input line, and there are no default values for the parameters built in. This can be remedied by by using option equations like the options to tagit, or plot. The parameters will have default values, and so can be left out if not needed. Also the order in which options are specified is not important.
| > |
Making a diagram generator with optional parameters.
We can illustrate with the diagram generator used above.
| > | pic := proc(a,b,clr,eps) plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr),axes=none,scaling=constrained); end: |
| > |
We show a way to reduce the number of parameters in the procedure to two (a and b).
The parameters clr and eps are added to the local line. Also, two new local variables defaults and opts are added: defaults is set to a sequence of option equations, and opts is a list of the values of the optional parameters with the default values replaced by any value given by an option equation at the call. Note the use of subs and select to do this. Then the values of the parameters clr and eps are set from opts. The command select(type,[args],`=`) take the arguments to pic, selects out the ones which are of type `=` (that is the equations in the input line). This returns a list (which may be empty), so op removes the enclosing square brackets and then result is joined with defaults to make a list of equations which are substituted into the list of left hand sides of the option equations. This is done from left to right, so any option equation which is input takes precedence over the default equation.
| > |
| > | pic := proc(a,b) local defaults,opts,clr,eps; defaults:= Color=yellow, Offset=.3; opts:= subs([ op(select(type,[args],`=`)),defaults],[Color,Offset]); clr := opts[1]: eps := opts[2]: plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr),axes=none,scaling=constrained); end: |
Now, if we wanted a blue triangle with the labels offset by .5 instead of .3, we would execute
| > | pic(3,8,Color=blue, Offset=.5); |
![[Maple Plot]](images/parameterize40.gif)
A problem generator with optional parameters
How would you modify the problem generator prob above to use this version of pic? This simplest way is to just have clr and esp be non-optional parameters to prob.
| > |
| > | prob:=proc(a,b,clr,eps) tagit(pic(a,b,Color=clr,Offset=eps),["The right triangle shown has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end: |
However, if you wanted to, you could make clr and eps optional parameters in prob also, just by adding the same lines to prob that were added to pic.
| > | prob:=proc(a,b) local defaults,opts,clr,eps; defaults:= Color=yellow, Offset=.3; opts:= subs([ op(select(type,[args],`=`)),defaults],[Color,Offset]); clr := opts[1]: eps := opts[2]: tagit(pic(a,b,Color=clr,Offset=eps),["The right triangle shown has height ",a," and hypotenuse ",b,"."],"Its area is ", _AC(2*sqrt(b^2-a^2)),", and its perimeter is ",_AC(a+sqrt(b^2-a^2)+a/2*sqrt(b^2-a^2))) end: |
Test this out
| > | prob(3,4,Color=blue); |
QM_[0.05;2*7^(1/2);3+5/2*7^(1/2)]
AH_[0]
![[Maple Plot]](images/parameterize41.gif)
The right triangle shown has height 3 and hypotenuse 4.
Its area is
AC_[5]
AH_[0]
, and its perimeter is
AC_[5]
SKIP_
| > |
Adding a Help= option to a generator
It may be useful in the future for both you and others who are using your generator to add a Help option. This is a simple text message explaining the syntax. It is similar to the mctools help, except it is part of the generator itself rather than a separate procedure. We illustrate by adding a help option to the diagram generator. As with each option, there is a new local variable, a new addition to the defaults line, another entry at the end of the list of options in the opts := line, and a new assignment of the local variable from that. In the help case, there is a conditional statement that is executed if help=yes. Note we use mcprint rather than print or lprint to display the help message. This is for cosmetic purposes.
| > |
| > | pic := proc(a,b) local defaults,opts,clr,eps,help; defaults:= Color=yellow, Offset=.3,Help=no; opts:= subs([ op(select(type,[args],`=`)),defaults],[Color,Offset,Help]); clr := opts[1]: eps := opts[2]: help:=opts[3]: if help=yes then mcprint("pic(a,b) draws a right triangle (with blue interior) having labelled leg a and hypotenuse b. The labels are offset by [-.3, 0] for a and [.3,.3] for b. Options: Color=yellow Offset=.3"); RETURN(NULL) fi; plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr),axes=none,scaling=constrained); end: |
| > |
Protecting yourself against bad calls to a diagram or problem generator
After you have constructed a generator, you may want to use it many times. Usually, you will discover that some ranges of values of the parameters should be avoided. You can add error traps to the generator to explain what ranges to avoid. For example, take the orginal diagram generator (without all the optional parameters).
| > | pic := proc(a,b,clr,eps) plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr), axes=none,scaling=constrained); end: |
Where does this go bad? That is what values of a and b won't give a picture? When b <= a, since b is the hypotenuse of a right triangle with leg a. We could put in a gentle reminder of that in case the user (including yourself) might (inadvertently) put in values with a > b.
| > | pic := proc(a,b,clr,eps) if a >= b then ERROR("The first argument must be smaller than the second.") fi: plots[display](PT([-eps,a/2],a),PT([sqrt(b^2-a^2)/2+eps,a/2+eps],b), plottools[polygon]([[0,0],[0,a],[sqrt(b^2-a^2),0]],color=clr), axes=none,scaling=constrained); end: |
So, if we try to execute
| > | pic(3,1,yellow,.3); |
Error, (in pic) The first argument must be smaller than the second.
| > |
Inverse problems/domain of a parameter
Suppose you have solved a problem with parameters and have a method for obtaining the solution in terms of a, b, and c. Then we can often solve one or more of the inverse problems you get by exchanging the solution with one of the parameters. If your method is an equation with the solution on one side by itself and the other side an expression in the parameters, then it we can solve the inverse problem by solving the equation for the desired parameter.
Example
Problem: Bill has a oranges and Sally has b apples. How many pieces of fruit do they have together?
Solution: Let x be the number of fruits. Then x = a + b.
An inverse problem: Sally has a apples. Bill and Sally together have b pieces of fruit. How many pieces of fruit does Bill have?
Soution: Let x be the number of fruits Bill has. Then b = a + x. So x = b - a.
Problem State and solve an inverse problem to the Bill father age problem Bill's age is a times his father's age. In 10 years, his age will be b times his fathers age his father's age. How old is Bill? Put it in your WHS homework, using the answer format _AS with 5 alternatives. Make 2 of the alternatives 'possible wrong answers', that is answers a student might make either carelessness or by poor understanding of the rules of algebra.
Another concept that arises when you are solving a parameterized problem is that of the domain of a parameter. By this, we mean the set of values of the parameter for which there is a solution to the problem. For example, in the oranges and aples problem above, the domain of a (and b too) is all non-negative integers. Here the domains of the parameters are independent of each other. In the inverse problem described above, however, a can be any non-negative integer, but b must be an integer no less than a. So the domain of b depends on a.
Problem: In your solution to the problem 'Suppose we replace the 1/2 in the problem by a parameter a. and the 2/3 by a parameter b. Solve the resulting parameterized problem. Make a problem generator for it and post two or three versions of the problem.', are the parameters a and b independent? Describe the domains of these parameters.
Writing parameterless problem generators
After you have worked with a problem generator for awhile and know the domain of the parameters, you can use the rand function to supply values for the parameters in the generator. This makes the problem generator completely automated.
For example, a simple problem generator with random supplied values would be one which as one to add 1 digit numbers.
| > | addem := proc() local a,b,f; f := rand(1..9); a := f(); b:=f(); tagit(["Find the sum: ",a," + ",b," = "],_AC(a+b)) end: |
| > | addem(); |
QM_[0.05;11]
AH_[0]
Find the sum: 6 + 5 =
AC_[5]
SKIP_
| > |
A more complicated example would be to turn carry (from a previous section) into a parameterless problem generator .
| > | carry := proc() local u,t,h,cu,ct,ch,randelt,a,b,c,d,e,f; randelt := proc(set) local f; f := rand(1..nops(set)); set[f()] end: a := randelt([seq(i,i=1..9)]); b := randelt([seq(i,i=0..9)]); #nonleading digits can be 0. c := randelt([seq(i,i=0..9)]); d := randelt([seq(i,i=1..9)]); e := randelt([seq(i,i=0..9)]); f := randelt([seq(i,i=0..9)]); u := irem(c+f,10): cu := iquo(c+f,10); t := irem(cu+b+e,10): ct := iquo(cu+b+e,10); h := irem(ct+a+d,10): ch := iquo(ct+a+d,10); tagit(standards="Can carry correctly.","Complete the addition. Put in the correct carrys, including 0.", _ATcross([["Carry:",[ch],[ct],[cu],""], ["","",a,b,c], ["","+",d,e,f], ["",[ch],[[h,h+randelt([-1,1,2])]],[t],[u]] ],txtboxsize=2)); end: |
Now we would test it by simply executing
| > | carry(); |
Writing a problem generator for adding m n-digit numbers.
We can write problem generators where some of the parameters are author supplied, and others are randomly chosen. For example, we can generalize the carry problem to one where we specifiy how many numbers we want to add and how many digits they should have. This could be done using matrices and vectors to store the data. We would use the linalg package. It has a word linalg[randmatrix] to generate random matrices.
| > | linalg[randmatrix](3,2,entries=rand(1..9)); |
![matrix([[7, 5], [5, 1], [5, 6]])](images/parameterize42.gif)
| > |
Here is one solution. The word map is used to check the problem, since the output from ATcross is so extemely ugly and hard to read. We have also inserted the standards= option in this problem.
| > | carryprob := proc(m,n) local A,sm,cr,hold,hnew,i,j; A := linalg[randmatrix](m,n,entries=rand(1..9)); sm := vector(n+1); cr := vector(n+1); hold:= 0; cr[n+1]:=hold: for i from 1 to n do sm[n-i+2] := irem(hold+add(A[j,n-i+1],j=1..m) ,10,'hold'); cr[n-i+1]:=hold; od; if hold=0 then sm[1]:= `` else sm[1]:= hold fi: print(map(evalm,[cr,A,sm])); |
| > | tagit(standards=["Can carry correctly."],"Complete the addition. Put in the correct carrys.", _ATcross([["Carry:",seq([cr[i]],i=1..n),""], seq(["","",seq(A[j,i],i=1..n)],j=1..m-1), ["","+",seq(A[m,i],i=1..n)], ["",sm[1],seq([sm[i]],i=2..n+1)] ],txtboxsize=2)); |
| > | end: |
| > |
To make a random problem for the student to add three 4-digit numbers, we would just execute
| > | carryprob(3,4); |
| > |
Adding hints and solutions to homeworks and problems
A timely hint can be a real help to a student in need, so it is in your interest and your students to provide hints and even solutions to some problems. This can be done several ways in WHS homework. One way is to insert a link to a video or audio file in the problem statement. Then, if the student has high speed access, or if the files are available locally (on a CD, hard, or floppy drive). Another way is to insert the hint in a sentence or two at the end of the problem, or in a text section before the start of the problem. You can also put the hint in a hidden section, so that the student has the choice of whether to read it, look at it, or listen to it.
| > |
Adding a video hint using the pocket video studio
It is very nice to be able to create short video clips of your hands writing while you are talking about the problem, perhaps giving the solution or giving a hint to the solution. Then you can put a link in the problem so that the student can access your hint if needed.
Here are the steps:
1 Decide what your hint will be. Maybe you could practice it a couple of times.
2. Use the studio to make the hint file
3. Copy the hint to a floppy or to a cd
4. Install the homework which links to the hint, using the answer header method. (see examples below).
Important! The header for a homework with video hints must contain the arguments [1;0,0;0;1] in order to access a file in the root of a local drive. Otherwise, WHS looks in a directory whose name is the homework identifier for the file.
5. Upload the hint to the video server with the homework selected. This is the button just below the Upload homework button in the Homework Installation table
6. Check to make sure the hint is accessible from the homework, on your browser, which should be IE6 or higher. If it isn't then put mathclass.org and mathclass.com in your list of trusted sites:
Tagging audio or video hints by hand.
If we tagged the problem by hand, we can just add the hint by hand. It can go in the answer header AH, as described in the author documentation. We show three positionings below. If you want other positionings, you may need to experiment.
A video hint inserted in a line above the statement of the problem.
QM_[0;5]
AH_[0]
AH_[3;addition.wmv;click]
AH_[0]
What is 2 + 3?
AC_[4]
SKIP_
The same hint inserted in the line below the problem.
QM_[0;5]
AH_[0]
What is 2 + 3?
AC_[4]
AH_[3;addition.wmv;click]
SKIP_
Here is the same hint inserted inline.
QM_[0;5]
AH_[0]
What is 2 + 3?
AH_[0;addition.wmv;click]
AH_[0]
AC_[4]
SKIP_
Tagging hints in tagit, using av_ and ah_
av_ is a MCtools word to add the answer header tag with a link to a video or audio file.
| > | mctools(av_); |
MCtools, version Oct 15 2003.
Sorry that's not in the list.
MCtools, version Oct 15 2003.
Current choices are [ARRW, Axes, BOXLENGTH_, CARR, DL, DV, ERROR_, GP, GP2, GP3, HARDCOPY_, Header, LATEX_, MC_constants, MM, PA, PC, PNUM_, PP, PT, addlink, addsectionhint, addvlink, ah_, colors, fill, hashang, htmltable, lineit, maketable, mcpiecewise, mcprint, mctools, printit, roundto, symbolize, tableit, tagit, zipit, zipp].
"mctools(X)" gives syntax and defaults for "X"
I will insert the hint into the problem using the MCtools word av_. Note the first argument of AH_ is a 3. This ensures that WHS puts the hint link on a newline after the problem.
| > |
| > | tagit("What is 2 + 3?",_AS([5,4,6,7]),av_("cathy.wmv","click for hint"),_TP()); |
QM_[0.05;5]
AH_[0]
What is 2 + 3?
AS_[6;5;7;4]
AH_[3;cathy.wmv;click for hint]
SKIP_
ah_ is a MCtools word to insert answer headers into a tagit line. Tagit inserts by default answer headers with an argument of 0. This can be changed with the brks= option.
In order to put the hint inline at the beginning of the problem, call it with a first argument of 0 and also insert another answer header just before the statement of the problem, using ah_(0).
| > | tagit(av_(0,"hint.wmv","click for hint"),ah_(0),"What is 2 + 3?", _AC(5)); |
QM_[0.05;5]
AH_[0]
AH_[0;hint.wmv;click for hint]
AH_[0]
What is 2 + 3?
AC_[5]
SKIP_
| > |
Problem. Create a video hint for one of the problems in your homework and install it.
Adding a hidden section or hyperlink to a homework by hand.
Hidden Sections
You may have a lot of introductory material which you would like the students to be able to access if they need it. This can be put in in a hidden section at the top.
Steps for adding a hidden section
1. Open the section,
2. add the material,
3. then close the section
4. then export it to html.
Be sure the section is between the header tag and the skip tag, so it will show up in the posted homework. You can also insert hidden sections into problems by this method.
But, and this is important,
in order for the hidden sections to be accessible, you need to put your
magic number
into the zipit line with the
Magic=
option when you zip up the homework. The correct syntax is:
zipit("first","u://firstwhs",Magic=xxx);
where xxx is your magic number
Your magic number is your acctId number. If you are logged in to mathclass, you can view the source html of the mathclass page and look about 50 lines down for the string 'var acctId = xxx'. The xxx is your magic number.
Hyperlinks to external material
You can also put in a hyperlink to some material in the top section. For example, if you want to point your students to the Dr. Math page, you can use the insert menu at the top of maple to put the link in.
Steps for adding a hyperlink, using the Dr. Math hyperlink as an example.
1. Put your cursor at the top of the homework (between the header tag and the skip tag) where you want the link to appear,
2. then click the Insert menu,
3. then choose hyperlink ,
4. then in the box that appears type the link http://mathforum.org/dr.math/ and the text you want to appear in the hyperlink (something like Click here for Dr. Math will do).
Adding a hidden section or hyperlink in a problem via tagit.
To add a hint in a hidden section in a problem, we can do this by hand or using the MCtools word addsectionhint. In order for either of these to work correctly, it is necessary to know your Magic number (your author id number). See below.
Steps to add a hidden section by hand.
1. Create the section with the hint above the tagit line which generates the problem.
2. then close it and copy and paste the section into the formatted problem.
Be sure to put it above the skip tag and two lines below the answer line.
Important:
If your problem is parameterized and you have several instances of it, you will have to paste the section into each instance of the problem if you want the hint to occur in each version of the homework.
Also, if you update the problem by rexecuting the tagit line, you will have to remove by hand the skip that is generated.
Example: We have created the hidden hint section above the tagit line.
| > |
Bill mows 1/3 yard per hour. Sam mows 1/5 yard per hour. So together they mow 1/3 + 1/5 = 8/15 yard per hour.
| > | simp := proc(a,b) tagit("Write the following expression as a simple fraction:",a+b/a, _ALlabels([(a^2+b)/a, (a+b)/a,b,"none of the others"])) end: |
| > | simp(x,y); |
QM_[0.05;B]
AH_[0]
Write the following expression as a simple fraction:
![]()
lt_table gt_tr_
lt_td valign=middle gt_
lt_font color=red gt_ lt_b gt_A. lt_/b gt_ amp_nbsp lt_/font gt_
dt_lt_td valign=middle gt_
![]()
dt_
lt_td valign=middle gt_
lt_font color=red gt_ lt_b gt_B. lt_/b gt_ amp_nbsp lt_/font gt_
dt_lt_td valign=middle gt_
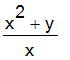
dt_
lt_td valign=middle gt_
lt_font color=red gt_ lt_b gt_C. lt_/b gt_ amp_nbsp lt_/font gt_
dt_lt_td valign=middle gt_
![]()
dt_
lt_td valign=middle gt_
lt_font color=red gt_ lt_b gt_D. lt_/b gt_ amp_nbsp lt_/font gt_
dt_lt_td valign=middle gt_
none of the others
dt_
rt_lt_/table gt_
AL_[A;B;C;D]
SKIP_
Adding a hidden section using addsectionhint:
Addsectionhint is a MCtools word that takes 2 arguments:
Here is what mctools() says about it.
| > | mctools(addsectionhint); |
MCtools, version Oct 15 2003.
addsectionhint(message,sectionmaterial), where title is the clickable message,
and sectionmaterial is a list of strings, lists, and expressions. This word is
written to be used in the problem=, pretext=, and aftertext= environments,
but can be mcprinted outside those environments.
Important. This method requires that you use zipit with the option Magic=xxx , just as you must do when you add a hidden section by hand. Also, the word addsectionhint needs to be enclosed in single quotes. This delays execution of the word for one step.
| > |
| > | simp := proc(a,b) tagit("Write the following expression as a simple fraction:",b+ a+b/a, _ALlabels([(b*a+a^2+b)/a, (a*b+b)/a,(2*b+a)/a,"none of the others"]), addsectionhint("click for hint",["Write each term as a fraction with denominator ",a,"."],"") ) end: |
| > |
| > | simp(2,5); |
QM_[0.05;A]
AH_[0]
Write the following expression as a simple fraction:
![]()
lt_table gt_lt_tr gt_lt_td valign="middle" gt_ lt_font color="red" gt_ lt_b gt_A. lt_/b gt_ amp_nbsp; lt_/font gt_lt_/td gt_
lt_td valign="middle" gt_
![]()
lt_/td gt_
lt_td valign="middle" gt_lt_font color="red" gt_lt_b gt_ amp_nbsp; B. lt_/b gt_ amp_nbsp; lt_/font gt_lt_/td gt_
lt_td valign="middle" gt_
![]()
lt_/td gt_
lt_td valign="middle" gt_lt_font color="red" gt_lt_b gt_ amp_nbsp; C. lt_/b gt_ amp_nbsp; lt_/font gt_lt_/td gt_
lt_td valign="middle" gt_
![]()
lt_/td gt_
lt_td valign="middle" gt_lt_font color="red" gt_lt_b gt_ amp_nbsp; D. lt_/b gt_ amp_nbsp; lt_/font gt_lt_/td gt_
lt_td valign="middle" gt_
none of the others
lt_/td gt_
lt_/tr gt_lt_/table gt_
AL_[A;B;C;D]
BEGINHINT_hint579030892800_click for hint_
Write each term as a fraction with denominator 2.
ENDHINT_hint579030892800_
SKIP_
| > |
Adding a hyperlink using addlink
Addlink is an MCtools word for adding a hyperlink to a problem.
| > | mctools(addlink); |
MCtools, version Oct 15 2003.
addlink(url,title), where url is the full path to the hyperlink
(except for http://), and title is the text to be clicked. If the file is in the homework
zipfile, then start the url with the string local:
This word is written to be used in the problem=, pretext=, and aftertext= environments,
but can be mcprinted outside those environments.
| > | tagit(addlink("msc.uky.edu/carl/ma310","Click here for help"),"Bill can mow a yard in 3 hours. Sam can mow it in 5. How long will it take them if they mow together?", _AC(1/(1/3+1/5))); |
QM_[0.05;15/8]
AH_[0]
lt_a href="http://msc.uky.edu/carl/ma310" gt_ Click here for help lt_/a gt_
Bill can mow a yard in 3 hours. Sam can mow it in 5. How long will it take them if they mow together?
AC_[5]
SKIP_
| > |