hyperb2.html

A drawing package for Poincare's disk model of the hyperbolic plane

by Carl Eberhart

When the parallel axiom of Euclidean plane geometry is replaced with one of its denials (namely, there is a line and point not on it such that there are at least two lines through the point which are parallel with the line), a perfectly consistent set of axioms for a different geometry (called hyperbolic geometry) results. One the models for this geometry is the Poincare circle model. a point (referred to as an hpoint below) is defined as a complex number of absolute value less than 1, a line (called hline below) is defined as the 'points' on a circle orthogonal to the unit circle or as the 'points' on a diameter of the unit circle. In the hyperb package, we develop a Maple vocabulary for drawing figures in this geometry. The we use this package to work on some problems in hyperbolic geometry.

Click here to download the worksheet

>

the basic hyperb package

> hyperb := table([]):

Drawpts takes a list of complex numbers and plots them. We will use it mostly to draw points in the Poincare model, but it does not object to drawing any numbers.

> hyperb[drawpts] := proc (z)
local opts, i;
opts := op(select(type,[args],`=`));
plot([seq([[Re(z[i]), Im(z[i])]],i = 1 .. nops(z))],style = point,
symbol = circle,color = red,scaling = constrained,opts)
end: with(hyperb);

world draws the poincare disk model (in yellow, if you want a different color, you can change it.)

> with(hyperb);

> hyperb[world]:= proc()
local opts;
opts := op(select(type,[args],`=`));
plots[display](plottools[disk](1,color=yellow,opts),opts)
end:
with(hyperb);

>

Problem. Given two hpoints z1 and z2 in the which do not lie on a diameter, show that there is a unique circle containing z1 and z2 which is orthogonal to the unit circle. Thus two hpoints determine an hline.

Solution. Let a and b, c and d be the real and imaginary parts of z1 and z2 respectively.

> z1 := a+b*I;

> z2 := c+d*I;

Now, any circle orthogonal to the unit circle through z1 also passes through . (This is a theorem. If you don't know it, work out the proof.) Hence the center w of the circle passing through z1, z2 and 1/conjugate(z1) lies on each of the perpendicular bisectors of the chords z1 to z2 and z1 to 1/conjugate(z1). This gives one complex equation with unknown real scalars s and t.

> eq:=evalc(1/2*(z1+1/conjugate(z1))+ t*I*(z1-1/conjugate(z1)) =1/2*(z1+z2)-s*I*(z1-z2));

>

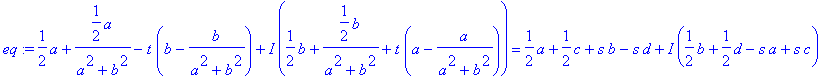
Actually this is two real equations in s and t.

> eqs := {evalc(Re(lhs(eq)-rhs(eq))),evalc(Im(lhs(eq)-rhs(eq)))};

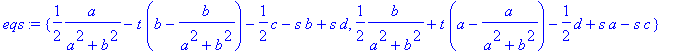
$eqs := {1/2*a/(a^2+b^2)-t*(b-b/(a^2+b^2))-1/2*c-s*b...$

Solving for s and t.

> sol:=solve(eqs,{s,t});

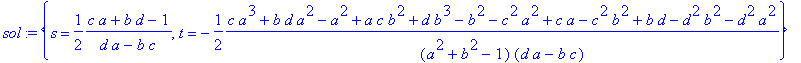
Now we can substitute the value for s into the rhs (right hand side) of eq to get w.

>

> hyperb[cen]:=unapply(evalc(simplify(evalc(subs(sol,1/2*(z1+z2)-s*I*(z1-z2))))),a,b,c,d);
with(hyperb);

Checking this out to make certain we have the correct formula for w,

> pt1 := .1+.7*I: pt2 := .8-.1*I: m := evalc(.5*(pt1+pt2));
pt3 := cen(Re(pt1),Im(pt1),Re(pt2),Im(pt2));
r := abs(pt3-pt1);

> plots[display]([world(),drawpts([pt1,pt2,m,pt3]),
plot([[Re(pt1),Im(pt1)],[Re(pt2),Im(pt2)]],color=blue),
plot([[Re(m),Im(m)],[Re(pt3),Im(pt3)]],color=blue)],scaling=constrained);

Looks good to me.

>

midpt takes two hpoints z1 and and computes the euclidean midpoint of the hline containing z1 and z2. If z1 and z2 lie on a diameter, the the midpoint is just the average of the z1 and z2. Otherwise, the center w and radius r of the circle containing the hline through z1 and z2 are computed, then used to compute the midpoint , where l is the distance from the center w to the average of z1 and z2.

>

> hyperb[midpt] := proc(z1,z2)
local a,b,c,d,w,r,l;
a := evalc(Re(z1)); b := evalc(Im(z1));
c := evalc(Re(z2)); d := evalc(Im(z2));
if a*d - b*c = 0 then w := evalc(1/2*(z1+z2)) else
w := cen(a,b,c,d);
r := abs(z1-w );
l := abs(1/2*(z1+z2)-w);
evalc(w + r/l*(1/2*(z1+z2)-w)) fi;
end:
with(hyperb);

>

> pt1 := .1+.8*I: pt2 := .7-.1*I: m := evalc(.5*(pt1+pt2));
pt3 := cen(Re(pt1),Im(pt1),Re(pt2),Im(pt2));
r := abs(pt3-pt1);
pt4:=midpt(pt1,pt2);

> plots[display]([world(),drawpts([pt1,pt2,m,pt3,pt4]),
plot([[Re(pt1),Im(pt1)],[Re(pt2),Im(pt2)]],color=blue),
plot([[Re(m),Im(m)],[Re(pt3),Im(pt3)]],color=blue)],scaling=constrained);

seg takes two hpoint z1 and z2 and draws an approximation to the hsegment connecting z1 and z2. It makes three calls to midpt. and constructs a sequence of points along the hsegment connecting z1 and z2, then draws the polygonal line connecting those points. Unless you look real close you can hardly tell it from the real thing, and it is fast. Note: There is a bug which occasionally pops up in seg. A more efficient (and accurate seg (seg2) is defined below.

>

> hyperb[seg] := proc(z1,z2)
local lst,z,nst,i,j,opts,n,margs;
opts := op(select(type,[args],`=`));
margs := remove(type, [args], `=`);
if nops(margs) >2 then n := margs[3] else n := 3 fi;
lst := evalf(z1),evalf(z2);
for i from 1 to n do
nst := lst[1]:
for j from 1 to nops([lst])-1 do
nst := nst,midpt(lst[j],lst[j+1]),lst[j+1];
od;
lst := nst;
od;
lst := map(evalc,[seq([Re(nst[i]),Im(nst[i])],i=1..nops([nst]))]);
plot(lst,thickness=2,opts);
end:

with(hyperb);

> pt1 := .1+.8*I: pt2 := .7-.1*I: m := evalc(.5*(pt1+pt2));
pt3 := cen(Re(pt1),Im(pt1),Re(pt2),Im(pt2));
r := abs(pt3-pt1);
pt4:=midpt(pt1,pt2);

> plots[display]([seg(pt1,pt2),world(),drawpts([pt1,pt2,m,pt3,pt4]),
plot([[Re(pt1),Im(pt1)],[Re(pt2),Im(pt2)]],color=blue),
plot([[Re(m),Im(m)],[Re(pt3),Im(pt3)]],color=blue)],scaling=constrained);

Here is word to draw the whole circle through z1 and z2 which is perpendicular to the unit circle

>

> hyperb[drawline] := proc(z1,z2)
local a,b,c,d,w,r,l,opts;
opts := op(select(type,[args],`=`));
a := evalc(Re(z1)); b := evalc(Im(z1));
c := evalc(Re(z2)); d := evalc(Im(z2));
w := cen(a,b,c,d);
w := [evalc(Re(w)),evalc(Im(w))];
print(w); r := sqrt((a-w[1])^2 + (b-w[2])^2);
plot([w[1]+r*cos(t),w[2]+r*sin(t),t=0..2*Pi],opts);
end:
with(hyperb);

>

> pt1 := .1+.8*I: pt2 := .7-.1*I: m := evalc(.5*(pt1+pt2));
pt3 := cen(Re(pt1),Im(pt1),Re(pt2),Im(pt2));
r := abs(pt3-pt1);
pt4:=midpt(pt1,pt2);

> plots[display]([drawline(pt1,pt2),seg(pt1,pt2),world(),drawpts([pt1,pt2,m,pt3,pt4]),
plot([[Re(pt1),Im(pt1)],[Re(pt2),Im(pt2)]],color=blue),
plot([[Re(m),Im(m)],[Re(pt3),Im(pt3)]],color=blue)],scaling=constrained);

>

Here is a word to generate a random hpoint.

> hyperb[randpt] := proc()
local a,b,f;
f := rand(-1000..1000);
a := 1000: b := 1000:
while (a^2 + b^2) >= 1000^2 do
a := f(): b := f();
od;
a/1000+b/1000*I
end:
with(hyperb);

>

Here is a word to generate a list of n random hpoints.

> hyperb[randpts] :=proc(n)
local i;
[seq(randpt(),i=1..n)]
end:
with(hyperb);

>

Here is a word to draw a broken line of hsegments. Actually, you can use it to draw an htriangle.

>

> hyperb[brknln]:= proc(l)
local i,opts;
opts := op(select(type,[args],`=`));
plots[display]([seq(seg(l[i],l[i+1],opts),i=1..nops(l)-1)]);
end:
with(hyperb);

> plots[display]([world(),brknln([.2+.3*I,-.7,-.8*I,.2+.3*I])],scaling=constrained);

>

Here is a word to draw an htriangle.

> hyperb[tri] := proc(z1,z2,z3)
local lst, nst,i,j,opts,cen;
opts := op(select(type,[args],`=`));
lst := evalf(z1),evalf(z2),evalf(z3),evalf(z1);
for i from 1 to 3 do
nst := lst[1]:
for j from 1 to nops([lst])-1 do
nst := nst,midpt(lst[j],lst[j+1]),lst[j+1];
od;
lst := nst;
od;
#cen := evalf(evalc(1/3*(z1+z2+z3)));
#lst := map(evalc,[seq([Re(nst[i]),Im(nst[i])],i=1..nops([nst]))]);
#plots[polygonplot]({seq([[evalc(Re(cen)),evalc(Im(cen))],lst[i ],lst[i+1]],i=1..nops(lst)-1)},color=blue,style=patchnogrid,opts):
brknln([lst ,lst[-1]],color=blue,opts)
end:
with(hyperb);

> plots[display]([world(),tri(-.2,-.7*I,.3+.3*I)],scaling=constrained);

>

Here is a word to draw a regular ngon around 0.

>

> hyperb[ngon]:= proc(r,n)
local i,opts,z1,z2,fig,margs;
opts := op(select(type,[args],`=`));
margs := remove(type, [args], `=`);
fig:=evalf([seq(op([r*cos(i*2*Pi/n)+I*r*sin(i*2*Pi/n),
r*cos((i+1)*2*Pi/n)+I*r*sin((i+1)*2*Pi/n)]),i=0..n)]);
if nops(margs) >= 3 then z1 := margs[3]; z2 := margs[4];
fig := [reflect(z1,z2,fig)] fi;
plots[display](brknln(fig,color=blue,opts), scaling=constrained,opts);
end:
with(hyperb);

> plots[display]([world(),ngon(.7,3,color=blue)],scaling=constrained);

Hyperbolic motions.

The analogue of the reflection about a line in the Euclidean plane is inversion about the hline z1z2 in the poincare disk, which we call a hyperbolic reflection . If the line is a diameter, then the reflection is an ordinary reflection, performed by the reflection matrix 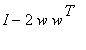where w is the unit column vector perpendicular to the diameter, 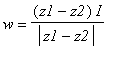. Otherwise the reflection takes z to 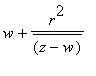= 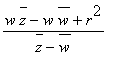where w is the center of the circle containing the hline and r is its radius. This is an extended Mobius map, in fact, it is the composition of three EM maps, first translation by -w which moves w to 0, then inversion about the circle of radius r (this is 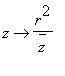), and last translation by w which moves 0 back to w. From this it follows that the map takes the unit circle onto itself, is fixed on the hline z1z2, interchanges each hpoint on one hside of the hline z1z2 with an hpoint on the other hside of z1z2, and takes hlines to hlines. Further down, we define a distance function on the poincare disk such that the reflection defined here is a rigid motion.

>

Here is a word to perform this reflection on each point of fig, a list of hpoints.

> hyperb[reflect]:= proc(z1,z2,fig)
local a,b,c,d,w,r,l,z, M;
a := evalc(Re(z1)); b := evalc(Im(z1));
c := evalc(Re(z2)); d := evalc(Im(z2));
if a*d - b*c = 0 then w := evalc(I*(z1-z2));
w := evalc(w/abs(w));
w := matrix(2,1,[evalc(Re(w)),evalc(Im(w))]);
M := evalm(matrix(2,2,[1,0,0,1])-2*w&*linalg[transpose](w));
l := NULL;
for z in fig do
w := evalm(M&* [evalc(Re(z)),evalc(Im(z))]);
l := l,w[1]+I*w[2] od;
else
w := cen(a,b,c,d);
r := abs(z1-w);
l := NULL;
for z in fig do l := l,evalc(w+r^2/conjugate(z-w) ) od;
fi;
[l];
end:
with(hyperb);

> reflect(.1,-.1*I,[0]);

>

> plots[display]([world(),tri( -.3,-.7+.3*I,-.1-.8*I),tri(op(reflect(.1*I,.2,[-.3,-.7+.3*I,-.1-.8*I])))],scaling=constrained);

> plots[display]([world(),tri( -.3, -.7+.2*I,-.1-.8*I),tri(op(reflect(-.1*I,.01,[-.3,-.7+.2*I,-.1-.8*I])))],scaling=constrained);

>

A hyperbolic rotation.

Problem. Fix an hpoint z1 in the poincare disk. Define a map rot by 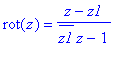. Show the following properties hold.

1. rot(rot(z)) = z for all z

2. If z is an hpoint, then so is rot(z).

3. Let f1 and f2 be the fixed points of rot. Show that f1 and f2 lie on the ray starting at 0 and passing through z1. Show further that 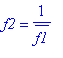, and that one of f1 and f2 is an hpoint (in fact, is between 0 and z1).

4. Show that hlines get carried onto hlines by rot.

Note if z1 = 0 then the map is and is a 180 degree rotation about 0.

>

> rot := (z,z1)->(z-z1)/(conjugate(z1)*z-1);

> solve(rot(z,.8)=z,z);

>

> hyperb[rotate] := proc(z1,fig)
local a;
a := z1;
map(z->(z-a)/(conjugate(a)*z-1),fig);
### WARNING: `z1` is a lexically scoped parameter
### WARNING: `z1` is a lexically scoped parameter
### WARNING: `a` is a lexically scoped local
end:
with(hyperb);

> hyperb[seg2] := proc(z1,z2)
local z3 ,lst,z,nst,i,j,opts,n,margs;
opts := op(select(type,[args],`=`));
margs := remove(type, [args], `=`);
if nops(margs) >2 then n := margs[3] else n := 10 fi;
z3 := op(rotate(z1,[z2]));
lst := [seq(evalf(evalc(i/n*z3)),i=0..n)];
nst := rotate(z1,lst);
lst := map(evalc,[seq([Re(nst[i]),Im(nst[i])],i=1..nops(nst))]);
plot(lst,thickness=1,opts);
end:
with(hyperb);

Definition. The hdistance between 0 and an hpoint z is defined to be hdist(0,z) = 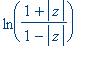. The hdistance between z1 and z2 is defined as the hdistance between 0 rot(z2), where rot is the hyperbolic rotation which exchanges 0 and z1.

Problem. Show the following.

1. As an hpoint z moves toward the unit circle,

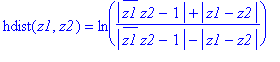
3. Hyperbolic reflections are hdistance preserving.

4. Hyperbolic rotations are hdistance preserving.

> evalc(rotate(1/10+1/2*I,[z]));

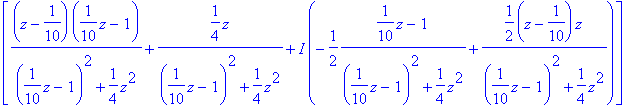
> f := z->evalc(op(rotate(1/10+1/2*I,(rotate(1/10+1/2*I,[z])))));

> simplify(f(x+I*y));

>

> hyperb[hdist] := proc(z1,z2)
ln((abs(conjugate(z1)*z2-1)+abs(z1-z2))/(abs(conjugate(z1)*z2-1)-abs(z1-z2)))
end:
with(hyperb);

> hdist('z1','z2');

>

Problem. Draw the hline through z1 and z2.

This can be solved with a hyperbolic rotation. Namely, We rotate z1 to 0, then draw the diameter (which is an hline) through 0 and rot(z2), then we apply rot again. The image of the diameter is the hline through z1 and z2.

>

> hyperb[hline] := proc(z1,z2)
local a,b,c,d,w,r,t,i,pts,z3,n,opts,margs;
opts := op(select(type,[args],`=`));
margs := remove(type, [args], `=`);
if nops(margs) >= 3 then n := margs[3] else n:= 10 fi;
a := evalc(Re(z1)); b := evalc(Im(z1));
c := evalc(Re(z2)); d := evalc(Im(z2));
if a*d - b*c = 0 then w := evalc(z1-z2);
w := evalc(w/abs(w));
r := evalc(Re(w)): t := evalc(Im(w)):
plot([[-r,-t],[r,t]],opts);
else
w := cen(a,b,c,d);
z3 := evalc(I*w/abs(w));
pts := [seq(evalf(evalc(i*z3/10)),i=-n..n)];
r := (abs(w)-abs(w-z1))/abs(w)*w;
pts :=map(z->(z-r)/(conjugate(r)*z-1),pts);
pts := [seq([evalc(Re(pts[i])),evalc(Im(pts[i]))],i=1..nops(pts))];
plot(pts,opts);
fi;
### WARNING: `r` is a lexically scoped local
end:

with(hyperb);

> plots[display]([world(),hline(.2,.3*I)],scaling=constrained);

Problem. Find the hyperbolic midpoint of a segment in the hyperbolic plane

This also is solved easily using the rotation. Rotate z1 to 0 and z2 to 2, measure the hdistance from 0 to a, find the hmidpoint of 0 to a, then rotate it back.

> hyperb[hmidpt] := proc(z1,z2)
local d,a,m,t;
a := op( rotate(z1,[z2]));
d := hdist(0,a);
m := max((solve(hdist(0,t*a)=d/2,t)))*a;
(op(rotate(z1,[m]))) end;
with(hyperb);

>

> hmidpt(9/10+1/10*I,9/10*I);

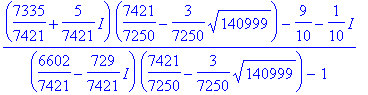
> p :=evalf(%);

Problem. Draw the hline through z1 perpendicular to the hline through z1 and z2.

> hyperb[hperp] := proc(z1,z2)
local z3,a,m,t,opts;
opts := op(select(type,[args],`=`));
a := op( rotate(z1,[z2]));
z3 := evalc(I*a);
z3:= op(rotate(z1,[z3]));
hline(z1,z3,opts)
end:
with(hyperb);

>

> plots[display]([world(),hline(.2,.6*I),hperp(.2,.6*I,color=blue,thickness=3)],scaling=constrained);

hyperbolic angles and the defect of a triangle.

Problem. Compute the hyperbolic angle z2 z1 z3

Solution. Rotate the vertex z1 to 0 and measure the resulting Euclidean angle.

> hyperb[hangle] := proc(z2,z1,z3)
local a,z4,z5;
a := op( rotate(z1,[z2,z3]));
linalg[angle](evalc([Re(a[1]),Im(a[1])]),evalc([Re(a[2]),Im(a[2])]));
end;
with(hyperb);

>

> hangle(1/10,1/20,1/10*I);

Problem. Find the defect of a triangle.

Solution . Easy using hangle.

> hyperb[defect] := proc(z1,z2,z3)
Pi-(hangle(z1,z2,z3)+hangle(z2,z3,z1)+hangle(z3,z1,z2)) end; with(hyperb);

> defect(8/10,0,9/10*I);

> evalf(%);

>

A quadrangle problem.

An interesting theorem about convex quadrangles in the Euclidean plane is that if the centers of the opposite exterior squares erected on the sides of the quadrangle are joined, the resulting two segements are of equal length and are perpendicular. We with to investigate the analogue in the hyperbolic plane.

First here is a word to draw a quadrangle.

> hyperb[quad] := proc(z1,z2,z3,z4)
local opts;
opts := op(select(type,[args],`=`));
plots[display]([ seg(z1,z2,opts),seg(z2,z3,opts),seg(z3,z4,opts),seg(z4,z1,opts)]) end:
with(hyperb);

> plots[display]([world(),quad(0,.6,.6+.6*I,.6*I)],scaling=constrained);

>

Next, there are no squares in the hyperbolic plane, so we need a hyperbolic analogue of square. The first thing that comes to mind is a quadrangle with two sides congruent to its base and perpendicular to it. Such a thing might be called a Sacchari square . Here is a word to draw a Sacchari square..

> hyperb[sacchari] := proc(z1,z2)
local a,b,c;
a := op(rotate(z1,[z2]));
b := evalc(a*I);
c := op(rotate(a,[evalc(-b)]));
[op(rotate(z1,[b])),z1,z2,op(rotate(z1,[c]))];
end:
with(hyperb);

>

> plots[display]([world(),quad(op(sacchari(-.3, 0)))],scaling=constrained);

Now we need a word to calculate the intersection of the diagonals of A Sacchari square: for such a point would be the center.

> hyperb[intsect] := proc(s1,s2)
local fig,w,t,sol,s,ts;
fig := rotate(s1[1],[s1[2],op(s2)]);
if evalc(Re(fig[2])*Im(fig[3])-Im(fig[2])*Re(fig[3]))=0 then
if (evalc(fig[2])*evalc(fig[3]) = 0
or evalc(fig[2]/abs(fig[2]) + fig[3]/abs(fig[3])) = 0) then RETURN(0) fi
else
w := cen(evalc(Re(fig[2])),evalc(Im(fig[2])),evalc(Re(fig[3])),evalc(Im(fig[3]))) fi;
assume(t,real);
additionally(t >=0);
additionally(t<=1);
ts := 0;
sol :=
[fsolve(conjugate(w-fig[2])*(w-fig[2])= conjugate(w-t*fig[1])*(w-t*fig[1]),t)];
for s in sol do if s >=0 and s <= 1 then ts := s fi od;
op(rotate(s1[1],[evalc(ts * fig[1])]));
end:
with(hyperb);

> intsect([-.1*I,.1*I],[.1 ,-.1]);

Next, we define a word to take a quadrangle and draw the sacchari squares on its edges, then draw the two segments in question and print the difference in the lengths of the segments. We can then examine visually to see if the segments are perpendicular

> drawit := proc(z1,z2,z3,z4)
local s1,s2,s3,s4,z5,z6,z7,z8,opts,l1,l2;
opts := op(select(type,[args],`=`));
s1 := sacchari(z2,z1);
z5 := intsect([s1[1],s1[3]],[s1[2],s1[4]]);
s2 := sacchari(z3,z2);
z6 := intsect([s2[1],s2[3]],[s2[2],s2[4]]);
s3 := sacchari(z4,z3);
z7 := intsect([s3[1],s3[3]],[s3[2],s3[4]]);
s4 := sacchari(z1,z4);
z8 := intsect([s4[1],s4[3]],[s4[2],s4[4]]);
plots[display]([world(color=turquoise),drawpts([z1,z2,z3,z4,z5,z6,z7,z8]),quad(z1,z2,z3,z4),
quad(op(s1),color=magenta),quad(op(s2),color=tan),quad(op(s3),color=sienna),quad(op(s4),color=black),seg(z5,z7,color=blue),seg(z6,z8,color=blue)],scaling=constrained,title=convert(hdist(z5,z7)-hdist(z6,z8),string),opts);
end:

> frame := t -> drawit(-t-t*I,t-t*I,t+t*I,t*I);

> frame(.5);

>

So this analogue of the quadrangle theorem is false all around. The segments do not have to be perpendicular not do they have to be the same length.

Another analogue of square would be an equiangular, equilateral 4 gon. As in the case of equiangular triangle, there is exactly one equiangular 4-gon with a given side.

>

> hyperb[hsquare] := proc(z1,z2)
local t,z3,fig,m;
t := fsolve(hdist(t,t*I)=hdist(z1,z2),t,0..1);
z3 := op(rotate(z1,[z2]));
fig := rotate(t,[t*I,-t,-t*I]);
m := evalc((fig[1]+z3)*.5);
rotate(z1,[0,z3,op(reflect(0,m,[fig[2],fig[3]]))]);
end:

> with(hyperb);

> quad(op(hsquare(.3,-.2)));

> drawit2 := proc(z1,z2,z3,z4)
local s1,s2,s3,s4,z5,z6,z7,z8,opts,l1,l2;
opts := op(select(type,[args],`=`));
s1 := hsquare(z1,z2);
z5 := intsect([s1[1],s1[3]],[s1[2],s1[4]]);
s2 := hsquare(z2,z3);
z6 := intsect([s2[1],s2[3]],[s2[2],s2[4]]);
s3 := hsquare(z3,z4);
z7 := intsect([s3[1],s3[3]],[s3[2],s3[4]]);
s4 := hsquare(z4,z1);
z8 := intsect([s4[1],s4[3]],[s4[2],s4[4]]);
plots[display]([world(color=turquoise),drawpts([z1,z2,z3,z4,z5,z6,z7,z8]),quad(z1,z2,z3,z4),
quad(op(s1),color=magenta),quad(op(s2),color=tan),quad(op(s3),color=sienna),quad(op(s4),color=black),seg(z5,z7,color=blue),seg(z6,z8,color=blue)],scaling=constrained,title=convert(hdist(z5,z7)-hdist(z6,z8),string),opts);
end:

> frame := t -> drawit2(-t-t*I,t-t*I,t+t*I,t*I);

>

> frame(.5);

So its not true for this analogue either! Well, I didn't really expect it to be.

Coloring a hyperbolic triangle

It would be nice to color the interior of a hyperbolic triangle. In order to do this, one needs to 'triangulate' the interior that the interiors of these triangles nearly covers the interior of the hyperbolic triangle without covering any of its exterior. If one could find a point p in the interior so that each point on the triangle can be seen from p (ie the segment to p lies in the interior) then it would be easy. The Euclidean centroid of [z1,z2,z3] (the average of z1,z2, and z3) might not even lie in the interior of the hyperbolic triangle. But the the hyperbolic centroid (the intersection of the hyperbolic medians) does.

> hyperb[centroid]:=proc(z1,z2,z3)
local m1,m2;
m1 := hmidpt(z1,z2);
m2 := hmidpt(z2,z3);
intsect([z3,m1],[z1,m2]);
end:
with(hyperb);

> hyperb[medians] := proc(z1,z2,z3)
local m1,m2,m3;
m1 := hmidpt(z1,z2);
m2 := hmidpt(z2,z3);
m3 := hmidpt(z1,z3);
plots[display]( [seg2 (z1,m2,7),seg2 (z2,m3,7),seg2 (z3,m1,7)]);
end:
with(hyperb);

> f := (z1,z2,z3) -> plots[display]([drawpts([centroid(z2,z1,z3)]),world(),tri(z1,z2,z3),medians(z1,z2,z3)],axes=none,scaling=constrained);

> f(-.95,-.3,-.75+.5*I);

However, we can see that the centroid cannot always see the vertices of the triangle.

We might also look at the incenter, which is the intersection of the angle bisectors.

>

> hyperb[anglebisector] := proc(z1,z2,z3)
local a,z4,z5,t;
a := op( rotate(z1,[z2,z3]));
z4 := evalf(evalc(a[2]*abs(a[1])/abs(a[2])));
z5 := op(rotate(z1,[evalc((a[1]+z4)/2)]));
end:
with(hyperb);

>

> anglebisector(-.1-.3*I,.1,.1*I);

> hyperb[incenter] := proc(z1,z2,z3)
local z4,z5;
z4 := anglebisector(z1,z2,z3);
z5:= anglebisector(z2,z3,z1);
intsect([z1,z4],[z2,z5])
end;
with(hyperb);

>

> incenter(.2-.4*I,.2,.7*I);

> hyperb[bisectors] := proc(z1,z2,z3)
local m1,m2,m3;
m1 := anglebisector( z1,z2,z3);
m2 := anglebisector(z2,z3,z1);
m3 := anglebisector(z3,z1,z2);
plots[display]( [seg2(z1,m1,20),seg2 (z2,m2,20),seg2(z3,m3,20)]);
end:
with(hyperb);

> f := (z1,z2,z3) -> plots[display]([drawpts([incenter(z2,z1,z3)]),world(),tri(z1,z2,z3),bisectors(z1,z2,z3)],axes=none,scaling=constrained);

> f(-.95,-.3,-.75+.5*I);

It looks like the incenter can see all three vertices here, however it is clear that it cannot see one in the triangle below.

> f(-.95,-.6,-.75+.5*I);

> f := (z1,z2,z3) -> plots[display]([world(),tri(z1,z2,z3)],axes=none,scaling=constrained);

In fact, we can see that by taking the triangle to be the one below that there is no point in the interior from which you can see all three vertices.

> f(-.95,-.7+.3*I,-.75+.5*I);

Here is a triangle coloring word which triangulates from the incenter.

> hyperb[stri] := proc(z1,z2,z3)
local lst, nst,i,j,opts,c,n,margs;
opts := op(select(type,[args],`=`));
margs := remove(type, [args], `=`);
lst := evalf(z1),evalf(z2),evalf(z3),evalf(z1);
if nops(margs)>3 then n := margs[4] else n := 3 fi;
for i from 1 to n do
nst := lst[1]:
for j from 1 to nops([lst])-1 do
nst := nst,midpt(lst[j],lst[j+1]),lst[j+1];
od;
lst := nst;
od;
c := incenter(op(evalf([z1,z2,z3])));
lst := map(evalc,[seq([Re(nst[i]),Im(nst[i])],i=1..nops([nst]))]);
plots[polygonplot]({ seq([[evalc(Re(c)),evalc(Im(c))],lst[i ],lst[i+1]],i=1..nops(lst)-1)},color=blue,style=patchnogrid,opts);
end:
with(hyperb);

Here is a word which takes a triangle and returns a list of 6 triangles all with the centroid as a common vertex.

>

> hyperb[barycentric] := proc(z1,z2,z3)
local c,m1,m2,m3;
m1 := hmidpt(z2,z3);
m2 := hmidpt(z1,z3);
m3 := hmidpt(z2,z1);
c := centroid(z1,z2,z3);
[[z1,c,m3],[m3,c,z2],[z2,c,m1],[m1,c,z3],[ z3,c,m2],[m2,c,z1]];
end:
with(hyperb);

>

> zs := evalf(randpts(3));

> m1 := anglebisector(zs[1],zs[2],zs[3]);
m2 := anglebisector(zs[2],zs[3],zs[1]);

> c:=intsect([zs[1],m1],[zs[2],m2]);

> pl:= plots[display]([drawpts([m1,m2,c]),stri(op(zs),4)],scaling=constrained):

> pl;

>

> cmplxtransform := proc(g)
plottools[transform](unapply([evalc(Re(g)),evalc(Im(g))],x,y));
end;

> g := op(reflect(.2,.3*I,[x+I*y]));

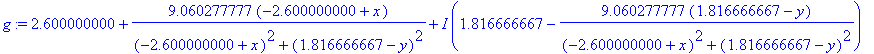
> h :=unapply([evalc(Re(g)),evalc(Im(g))],x,y);

> h(.2,.4);

>

> k := plottools[transform]((x,y)->h(x,y));

> f := cmplxtransform(op(reflect(.1+.2*I,-.1+.2*I,[x+I*y])));

>

> plots[display]([f(pl),pl,world()]);

> plots[display]([tri(op(zs)),world()]);

> plots[display]([seq(stri(op(tr)),tr=barycentric(op(zs))),world()],scaling=constrained);

Hyperbolic turtle graphics

The language Logo was developed several years ago as an educational tool. One of the more successful features it had was socalled turtle graphics. One imagined a turtle walking around dragging his tail to which a pen was tied. The command vocabulary was limited. st for start, pd for pen down, sh set heading, rt for turn right, fd for forward. But with that you could draw many interesting figures in the Euclidean plane, such as regular ngons, stars, as well as ramdom paths. Here is a a corresponding vocabulary for turtle graphics in the hyperbolic plane. Experiment with it. Can you draw a regular ngon with it?

>

> hyperb[st] := proc()
global hd,path,pencolor,lead,zp,penup,frame, movie,record;
pencolor:=blue; lead:= 2;
penup := false;
if nargs >0 then record := true; frame := world(); movie := frame; else record:= false fi;
path := 0,.0001*I;
zp := 0;
hd := 1;
end:
with(hyperb);

>

> hyperb[pd] := proc(bool)
global penup;
penup := bool;
end:
with(hyperb);

>

> hyperb[rt] := proc(theta)
global hd ;
local unit,b;
unit := (exp(1.)-1)/(exp(1.)+1);
b := evalf(evalc((path[-1]-path[-2])/
(conjugate(path[-1])*path[-2]-1))):
hd := evalf(evalc(b*(cos( theta)+ I*sin(theta))));
hd := evalc(hd/abs(hd));
end:
with(hyperb);

> hyperb[rt] := proc(theta)
global hd ;
local unit,b;
b := op(rotate(path[-1],[path[-2],path[-1]]));
unit := (exp(1.)-1)/(exp(1.)+1);
hd := evalf(evalc(b[1]*(cos( theta)+ I*sin(theta))));
hd := evalc(hd/abs(hd));
end:
with(hyperb);

Warning, the name rt has been redefined

>

> hyperb[sh] := proc(theta)
global hd;
hd := evalf(evalc((cos( theta)- I*sin(theta))*hd));
end:
with(hyperb);

>

> hyperb[fd] := proc(d)
local z,a,x;
global path,frame,movie,zp,pl,record;
a := zp;
z := evalf( evalc((exp(d)-1)/(exp(d)+1)*hd));
zp := evalf(evalc((z-a)/(conjugate(a)*z-1)));
path := path,zp;
#sh(0);
pl := seg(path[-2],path[-1], color=pencolor,thickness =lead);
frame := plots[display]([frame,pl]);
movie := movie,frame;
plots[display]([ frame,world()],scaling=constrained,axes=none );
end:
with(hyperb);

> hyperb[sp] := proc(pos)
global zp ;
zp := pos
end;
with(hyperb);

Now we do an interactive tour,

> st(0);

> sh(Pi/2);

> fd(1);

> pencolor:=magenta;

> printlevel:=1;

> rt(Pi/2);

> fd(1);

> rt(Pi/2);

> fd(1);

> pencolor:=red; lead := 3;

> rt(Pi/2); fd(1);

> sh(Pi);

> rt(-Pi/2);

> fd(1);

> rt(Pi); pencolor:= white; fd(2);

> lead :=1 ;

> pencolor:=tan; fd(1.2);

> plots[display]([movie],insequence=true,scaling=constrained,axes=none);

Problem. Draw a regular ngon starting from 0.

Solution. For a given distance d from 0, there is a unique angle such that each interior angle of the regular ngon with radius d is . The nicest regular ngon would be the one with radius d=1. To get the angle for n =

> z1 :=solve(hdist(t,0)=1,t)[1];

> ang := unapply(simplify(hangle(0,z1, z1*cos(2*Pi/n)+I*z1*sin(2*Pi/n))),n);

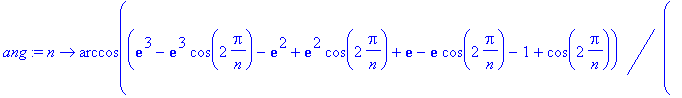
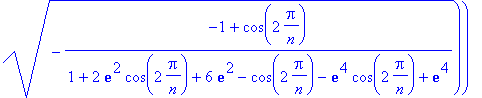
For example, for n = 5 the angle is

> a:=evalf(ang(5 ));

> evalf(180/Pi*a);

To get the side of this regular pentagon,

> s :=evalf(subs(n=5,hdist(z1,z1*cos(2*Pi/n)+I*z1*sin(2*Pi/n))));

So, to draw this thing from 0 go forward s, then left Pi-2*a (equivalently right 2, and repeat this 5 times.

> st(0);

> fd(-s);

> rt(Pi-2*a);

> fd(-s);

> plots[display]([movie],insequence=true,scaling=constrained,axes=none);

Tiling the hyperbolic plane with equilangular triangles.

Unlike the Euclidean plane the hyperbolic plane cannot be tiled with equiangular radians = 60 degree triangles. That's because there isn't any such triangle! All triangles have an angle sum less than Pi radians. However, for each n > 6, there is a unique equiangular triangle with each interior angle = radians, and this equilangular triangle can tile the hyperbolic plane. Below we use the hyperb package to do this for the case n = 7.

First find the side of the triangle.

> t7:=fsolve(hdist(t*cos(2/7*Pi)+I*t*sin(2/7*Pi),t)=hdist(0,t),t,.3.. .99);

Then construct 7 copies of the the triangle which have 0 as a common vertex.

> segs1 := seq([0,evalf(evalc(t7*(cos(i*2/7*Pi)+I*sin(i*2/7*Pi))))],i=0..6);

> segs2 := seq(evalf([ evalc(t7*(cos(i*2/7*Pi)+I*sin(i*2/7*Pi))),evalc(t7*(cos((i+1)*2/7*Pi)+I*sin((i+1)*2/7*Pi)))]),i=0..6):

> pl1:=plots[display]([seq(seg2(op(segs2[i])),i=1..7),seq(seg2(op(segs1[j])),j=1..7)]):

> pl1;

Next reflect this regular 7-gon about one of its sides and then reflect that about 2 of its sides.

> segs3 := evalf(seq(reflect(op(segs2[1]), (segs2[i])),i=1..7)):

> segs3 := segs3,evalf(seq(reflect(op(segs2[1]), (segs1[i])),i=1..7)):

> segs4 := evalf(seq(reflect(op(segs3[7]), segs3[i]),i=1..nops([segs3]))),segs3,
evalf(seq(reflect(op(segs3[2]), segs3[i]),i=1..nops([segs3]))):

> pl2:=plots[display]([seq(seg2(op(segs4[i]),color=blue),i=1..nops([segs4]))]):

> plots[display]([pl1,pl2],scaling=constrained,axes=none);

>

Next, reflect the first blue part about its remaining 4 free sides and color it magenta.

> segs10 :=
seq(reflect(op(segs3[3]), segs3[i]),i=1..nops([segs3])),
seq(reflect(op(segs3[4]), segs3[i]),i=1..nops([segs3])),
seq(reflect(op(segs3[5]), segs3[i]),i=1..nops([segs3])),
seq(reflect(op(segs3[6]), segs3[i]),i=1..nops([segs3])):

>

> pl9:=plots[display]([pl1,pl2,seq(seg2(op(segs10[i]),color=magenta),i=1..nops([segs10]))]):

> plots[display]([pl9],scaling=constrained,axes=none);

Next, rotate the this about 0 6 times by an angle of 2*Pi/7.

> pl4:=plots[display]([pl9,plottools[rotate]( pl9 ,evalf(2*Pi/7)),
plottools[rotate]( pl9 ,evalf(4*Pi/7)),
plottools[rotate]( pl9 ,evalf(6*Pi/7)),
plottools[rotate]( pl9 ,evalf(8*Pi/7)),
plottools[rotate]( pl9 ,evalf(10*Pi/7)),
plottools[rotate]( pl9 ,evalf(12*Pi/7))]):

> plots[display]([world(),pl4],scaling=constrained,axes=none);

>

This is not a complete tiling, but can be continued to produce a complete tiling. Notice that each vertex is the center of a regular 7-gon, but that the hyperbolic plane is not tiled with regular 7-gons. Similar tilings can be made for each n > 6. The other equiangular triangles, of which there are uncountably many, cannot tile the hyperbolic plane.

an 'addition' on the hyperbolic plane.

Problem. You can define a geometric addition of hpoints as follows: hadd(z,w) is the hpoint p on the ray from 0 through the hyperbolic midpoint q of the hyperbolic segment from z to w whose hyperbolic distance from 0 is twice the hyperbolic distance from q to 0. In terms of the functions defined above 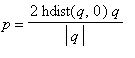, where q = hmidpt(z,w). This addition is clearly commutative, has an identity (0), and every hpoint z has an inverse relative to this identity (-z). Is it associative?

Solution. The function hadd defined below implements the definition of addition given above. The fucntion checkassoc is defined and a few calls to it convinces one that the operation is not associative.

> a := 'a':eqn:=t -> hdist(t,0) = .5*hdist(a,0);

> assume(a>0);

> h := unapply(solve(eqn(t),a),t);

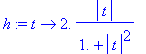
So we see that the point 2t/(1+t^2) is twice as far from 0 as t is for any t between 0 and 1. This enables us to define a doubling operator.

> hdouble := proc(z1)
local t,h;
h := proc (t) options operator, arrow; 2.*abs(t)/(1.+abs(t)^2) end proc;
h(abs(z1))*z1/abs(z1) end;

>

Once we have a doubling, we can define the addition

> hadd:= (z,w)-> hdouble(hmidpt(z,w));

Now checkass draws (a+b)+c and a+(b+c).

> checkass := proc(a,b,c)
local apbc, abpc;
abpc:= hadd(hadd(a,b),c);
apbc:= hadd(a,hadd(b,c));
print(apbc,abpc,evalc(abpc-apbc));
plots[display](world(),drawpts([apbc,abpc],color=blue),quad(0,c,abpc,hadd(a,b),color=blue),quad(0,hadd(b,c),apbc,a),
title=convert(err=hdist(hadd(hadd(a,b),c),hadd(a,hadd(b,c))),symbol),scaling=constrained) end;

>

> checkass(.8+.1*I,.9*I,-.8+.1*I);

Here we see that the results obtained by shifting parentheses are much different

>