GeoGebra Worksheet: TRISECTING A SEGMENT
This is the standard straightedge and compass technique for trisecting any line
segment. We will need the macro
that we will create later in another worksheet.
Start with three points, A,
B, and
C.
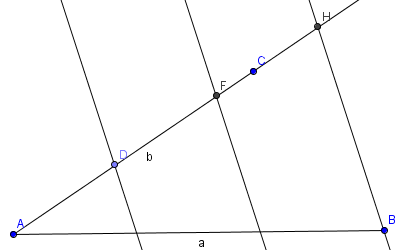
We will construct the points that divide
AB into three congruent segments.
- Uncheck VIEW-AXES.
- Select OPTIONS-LABELING-NEW POINTS ONLY.
-
Construct the ray, r(AC, emanating A and
passing through the point C.
Be sure that it passes through C
and not just close to C.
-
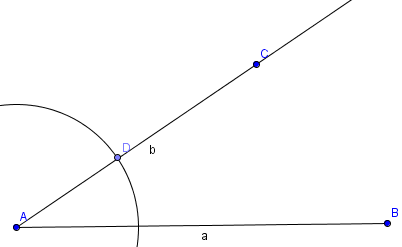
Use the "Circle with center
and point" tool
construct
a circle with center A and
intersecting r(AC) at a point
D:
-
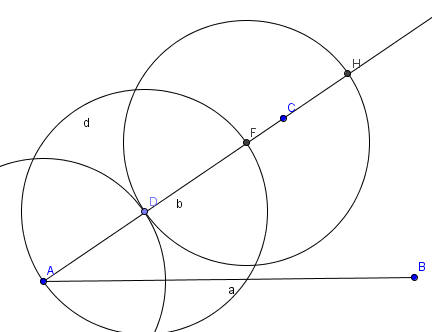
Construct the circle with center D
and passing through the point A.
This circle will have the same radius as the previous circle.
-
Find the intersection of the ray r(AC) with this circle,
label the point F.
-
Construct the circle with center F
and passing through the point D.
Use H to label the other
intersection of this circle with r(AC).
-
Construct the segment between B and
H,
BH.
-
Construct the line parallel to BH
passing through F.
-
Construct the line parallel to BH
passing through D.
-
Construct the points of intersection of these lines with the segment
AB.
-
Hide all lines, segments and circles.
-
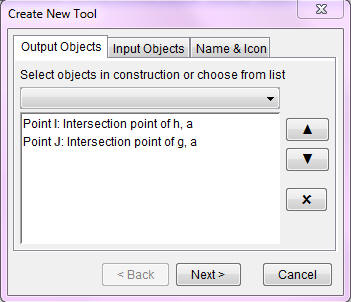
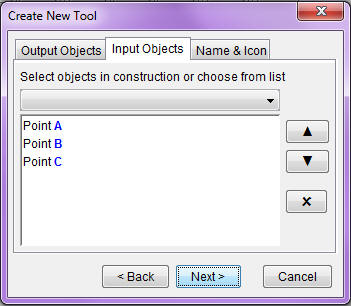
Construct a tool, called Trisect, which has the three
points A,
B, and
C as initial objects; and has the
two trisection points as the final objects.

A Triangle within a Triangle
-
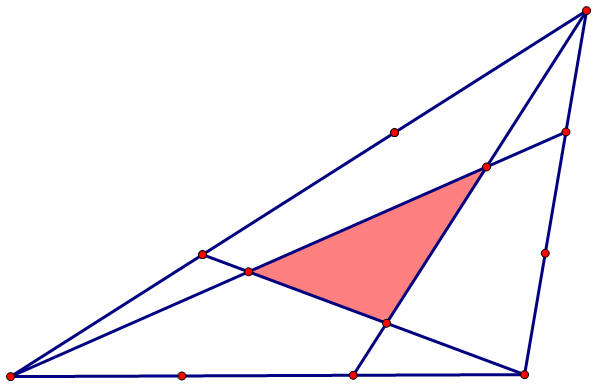
In this investigation we will investigate the area relationship between a
triangle and a triangle within it made by connecting each vertex with a
trisection point on the opposite side.
-
Construct a triangle
ΔABC using the Polygon Tool.
-
Use your trisect tool on the points A,
B, and
C (in that order), to trisect AB. Execute it again on
B,
C, and
A and
C,
A, and
B to trisect BC and AC.
-
Going clockwise around the triangle from
A to
B to
C, construct a segment from
A to the first point clockwise
past B, a segment from
B to the first point clockwise
from C, and a segment from
C to the first point clockwise
from A.
-
Construct the points of intersection of these segments. Label these
points D, E, and F.
-
Hide the segments and construct the triangle
ΔDEF using the Polygon Tool.
-
What is the relationship between the areas of the inner triangle and the
larger outer triangle. Can you guess
what the ratio of these areas is?
Can you compute this ratio? Find the area of triangle
ΔABC in your list (possibly poly1) and area of triangle
ΔDEF (possibly in poly2) in your list of Dependent
Objects.
- In the Input window at the bottom of the window, enter
Ratio = poly1/poly2. Find Ratio in your list of
Dependent Objects.
-
Name the file yourname_04.ggb
and email it to me by noon, Wednesday, September 8.