Gaussian Elimination

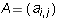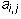Definition 1: A m by n matrix is a rectangular array of numbers with m rows and n columns. One can write for an m by n matrix where is the entry in row i and column j. Row i of the matrix is the 1 by n matrix 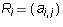whose entries are the entries of A with first index i. Similarly, column j is the m by 1 matrix consisting of the entries of A with second index j. Rows and columns are also referred to as row vectors and column vectors respectively. The leading column number of this row is the smallest index j with 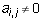or infinity if there is no such index. If the leading column number k of some row is finite, then column k is called a leading column.

Definition 2:The matrix 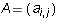is in echelon form if

1. The leading column number of rows 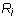which have at least one non-zero entry is a strictly increasing function of the row index .
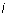2. If some row 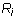has all its entries zero, then so does every row 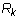with .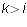

Definition 3:A matrix is in reduced echelon form if every leading column 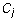has a unique non-zero entry and if this entry has value 1.

Of course, the non-zero entry must be in the row which has this column as its leading column.

Definition 4: An elementary row operation is any of the following functions from the set of m by n matrices to the set of m by n matrices:

1. Multiply every entry in a row by a non-zero number c.
2. Swap two different rows.
3. Replace a row with the sum of itself and a constant multiple of another row.

Notice that every elementary row operation has an inverse operation which is also an elementary row operation. For example, if c is the multiplier in the operation of type iii above, the inverse of that operation is one of the same type with multiplier -c.

Definition 5: Two matrices A and B are said to be row equivalent if there is a finite sequence of elementary row operations which maps A into B.

Clearly, two matrices can only be row equivalent if they have the same number of rows and the same numbeer of columns.

Exercise 1: Row equivalence is an equivalence relation, i.e.

1. (Reflexive) Every matrix A is row equivalent to itself.
2. (Symmetric) If a matrix A is row equivalent to a matrix B, then B is row equivalent to A.
3. (Transitive) If A is row equivalent to B and B is row equivalent to C, then A is row equivalent to C.

Because of Exercise 1, we know that the m by n matrices decomposes into a union of row equivalence classes, i.e. It is a disjoint union of sets 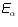where any two matrices are row equivalent if and only if they belong to the same one of these sets.

Definition 6: A row vector 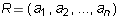is said to is said to be a linear combination of vectors 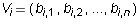if there are constants 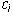such that 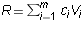, i.e. 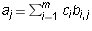for every .

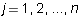Exercise 2: Let 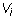be a finite set of vectors and S be the set of vectors which are linear combinations of the 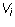. Show that S is closed under addition and multiplication by scalars.

In general, one would not expect the coefficients 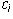to be uniquely determined, but it is true in the case where the 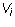are non-zero rows of a matrix in echelon form. In more detail:

Proposition 1: Let 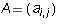be an m by n matrix in echelon form and 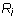for 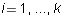be the rows of 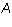which have at least one entry non-zero. If 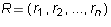is a linear combination of these rows, say, 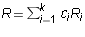, then there is a unique set of 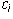for which this equation is true.

Proof: Suppose that j is the leading column number of row i. Then the equation says 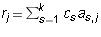. Now, 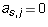for all 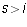because 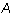is in echelon form and 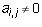because j is the leading column number of row i. This allows one to solve for a unique value of 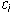in terms of the previous 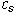(and the constants 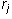and 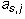). Since this is true for each i, the 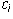are uniquely determined.

Things are particular simple in case of a matrix in reduced echelon form:

Corollary 1: If, in addition, the matrix 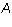is in reduced echelon form, then 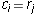where j is the leading column number of row i of .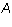

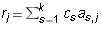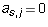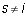Proof: The equation for column j is . One has for and 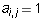. So the equation is just .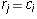

The leading column number of a linear combination of the rows of a matrix in echelon form is the leading column number of some row of that matrix (or infinity). More precisely:

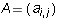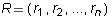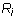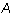Proposition 2: Let be an m by n matrix in echelon form and be a linear combination of the rows of . Then the leading column number of 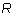is either infinity or equal to a leading column number of some row of .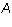

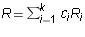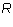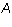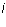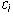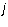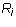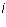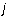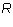Proof: Let express as a linear combination of the non-zero rows of . Let be the smallest index for which is non-zero and be the leading column number of . If does not exist or if the is infinity, then the leading column number of is infinite. Otherwise, we will show that 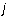is the leading column number of 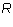. One has 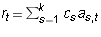. Suppose that .

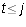1. If s is less than i, we have 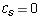and the corresponding term of the sum is zero.
2. If t is less than the leading column number of row s, then 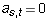and again the corresponding term of the sum is zero. Since the leading column number is an increasing function in a matrix in echelon form, we know that this is true whenever s is bigger than i (since 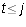) or when 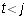and 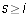. In particular, if 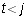, then every term of the sum is zero and so .
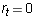3. If 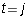, then the only term in the sum which could be non-zero is the term when s is i: 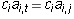. Since both factors are non-zero, the term is non-zero and so j is the leading column number of .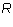

Gaussian elimination is essentially an algorithm for finding a reduced echelon matrix in the row equivalence class of a given matrix. More formally:

Proposition 3: Every row equivalence class contains at least one matrix in reduced echelon form.

Proof: See the textbook for the algorithm.

The main result of Chapter 1 of the text is the assertion that regardless of the sequence of elementary row operations, one always arrives at the same reduced echelon form matrix:

Theorem 1: Every row equivalence class contains exactly one matrix in reduced echelon form.

Proof: Suppose a row equivalence class contains two reduced echelon matrices A and B. There is a sequence of elementary row transformations which converts A into B. Each row of B is a linear combination of the non-zero rows of A and, similarly, each row of A is a linear combination of the non-zero rows of B. Since each non-zero row of B is a linear combination of the the rows of A, Proposition 2 says that the finite leading column numbers of B are amongst the finite leading column numbers of A. Similarly, the finite leading column numbers of A are amongst those of B.

The number of non-zero rows of A (or of B) is just the number of finite leading column numbers (because each non-zero row has a leading column number different from that of every other non-zero row). So, we know that A and B have the same zero rows. Further, because the leading column numbers are increasing functions of the row index, we know that a non-zero row of A has the same leading column number as the row of B with the same row index (and vice versa).

Suppose 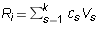expresses row i of A as a linear combination of the non-zero rows of B. By Corollary 1, we know that 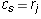where j is the leading column number of 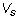. When s = i, this means that 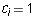because the leading column number of 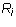is the same as that of 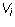and both A and B have entry 1 in that column. Otherwise, we know that 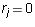because every entry of 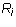is zero in all columns whose column index is the leading column number of another row. So, 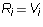for every i. But then A = B.