H_
Direct Sum Decomposition
In each of the problems with square check boxes, you need to
check all the correct answers in order for the answer to be marked correct.
SKIP_
p1
QM_[0;true;true;false;true]
In each case, decide if it is true that 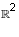 is the direct
sum of the subspaces U and V.
AH_[2]
is the direct
sum of the subspaces U and V.
AH_[2]
- U = {(a, 0) | a real} and V = {(a, -a) | a real}
AS_[true;false]
- U = {(a, -a) | a real} and V = {(a, a) | a real}
AS_[true;false]
- U = {(a, -a) | a real} and V = {(a-1;1-a) | a real}
AS_[true;false]
- U = {(a, b) | a, b real} and V = {(0, 0)}
AS_[true;false]
SKIP_
p2
QM_[0;is;is;is;is not]
Consider the subspaces U = {(a, 0) | a real}, V = {(0,b) | b real} and
W = {(c, c) | c real} of 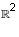 .
AH_[2]
.
AH_[2]
- The sum of any two of the subspaces
AS_[is;is not]
equal to the vector space
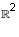 .
.
- The sum of all three of the subspaces
AS_[is;is not]
equal to the vector space
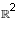 .
.
- The intersection of any two of the subspaces
AS_[is;is not]
the trivial subspace consisting of just {(0, 0)}.
- The vector space
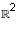 AS_[is;is not]
the direct sum of U, V, and W.
AS_[is;is not]
the direct sum of U, V, and W.
SKIP_
p3
QM_[0;true;true;true;true;true;true]
In this problem, we will be working in the vector space of all real valued
functions defined for all real numbers. Recall that such a function f(x)
is said to odd if f(-x) = -f(x) for all real x, and that it is
said to be even if f(-x) = f(x) for all real x. For example,
the sine function is odd and the cosine function is even. Indicate which
of the following are true; make sure you can either prove each assertion
or give a counter-example.
AH_[2]
- If f(x) is any real valued function defined for all real numbers, then
the function f(x) - f(-x) is an odd function.
AS_[true;false]
- If f(x) is any real valued function defined for all real numbers, then
the function f(x) + f(-x) is an even function.
AS_[true;false]
- The set U of odd real valued functions forms a vector subspace.
AS_[true;false]
- The set V of even real valued functions forms a vector subspace.
AS_[true;false]
- The vector space of all real valued functions is the sum
of U and V
AS_[true;false]
- The vector space of all real valued functions is the direct sum
of U and V
AS_[true;false]
SKIP_
p4
QM_[0;true;true;true;true;true]
Consider the vector space M of m by m square matrices. Recall that
a square matrix 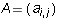 is said to be symmetric if
is said to be symmetric if
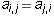 for all indices i and j. The same matrix is
said to be antisymmetric if
for all indices i and j. The same matrix is
said to be antisymmetric if 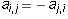 for all indices
i and j. Indicate which of the following are true; be sure that you
can either prove the assertion or give a counter-example.
AH_[2]
for all indices
i and j. Indicate which of the following are true; be sure that you
can either prove the assertion or give a counter-example.
AH_[2]
- If
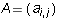 is anti-symmetric, then
is anti-symmetric, then 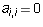 for all
indices i.
AS_[true;false]
for all
indices i.
AS_[true;false]
- The set U of symmetric m by m matrices is a vector subspace of M.
AS_[true;false]
- The set V of antisymmetric m by m matrices is a vector subspace of M.
AS_[true;false]
- M is the sum of U and V.
AS_[true;false]
- M is the direct sum of U and V.
AS_[true;false]
SKIP_
p5
QM_[0;true]
Let U be any subspace of a finite dimensional vector space V. Extend a
basis 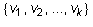 of U to a basis
of U to a basis 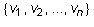 of V. Let W be the span of
of V. Let W be the span of 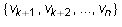 . Then V
is the direct sum of U and W
AS_[true;false]
Make sure you can either prove the assertion of give a counterexample.
SKIP_
p6
QM_[0;true;true]
Let U and W be arbitrary subspaces of a vector space V. Let
. Then V
is the direct sum of U and W
AS_[true;false]
Make sure you can either prove the assertion of give a counterexample.
SKIP_
p6
QM_[0;true;true]
Let U and W be arbitrary subspaces of a vector space V. Let 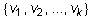 be a basis for the subspace
be a basis for the subspace 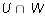 .
Extend this to a basis
.
Extend this to a basis 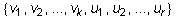 of U.
Extend the basis again to a basis
of U.
Extend the basis again to a basis 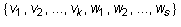 of W.
AH_[2]
of W.
AH_[2]
- The set
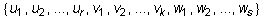 is a basis for U + W.
AS_[true;false]
is a basis for U + W.
AS_[true;false]
- dim(U + W) = dim(U) + dim(W) - dim(U
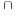 V).
AS_[true;false]
V).
AS_[true;false]
Make sure you can prove your assertions.
SKIP_
p7
QM_[0;yes]
Two subspaces U and W of 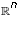 are said to be perpendicular to
each other if the dot product of any vector in U with any vector in V is
always zero. Is it true that, if U and W are perpendicular, then
U + W is the direct sum of U and W? Why?
AS_[yes;no]
SKIP_
p8
QM_[0;no;no]
Let U, V, and W be subspaces of vector space such that U + W = V + W.
AH_[2]
are said to be perpendicular to
each other if the dot product of any vector in U with any vector in V is
always zero. Is it true that, if U and W are perpendicular, then
U + W is the direct sum of U and W? Why?
AS_[yes;no]
SKIP_
p8
QM_[0;no;no]
Let U, V, and W be subspaces of vector space such that U + W = V + W.
AH_[2]
-
Does it follow that U = V?
AS_[yes;no]
-
Does it follow that U = V if the sum is direct?
AS_[yes;no]
Make sure you can either prove the assertion or give a counter-example.
SKIP_
p9
QM_[0;no]
Let U, V, and W be subspaces of a vector space. Suppose that for every two
of these subspaces, the sum of the two spaces is direct. Does it follow
that the sum of all three is direct?
AS_[yes;no]
Make sure you can either prove the assertion or give a counter-example.
SKIP_
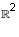 .
.
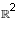 .
.
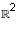 AS_[is;is not]
the direct sum of U, V, and W.
AS_[is;is not]
the direct sum of U, V, and W.
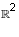 is the direct
sum of the subspaces U and V.
AH_[2]
is the direct
sum of the subspaces U and V.
AH_[2]
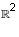 .
AH_[2]
.
AH_[2]
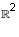 .
.
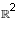 .
.
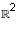 AS_[is;is not]
the direct sum of U, V, and W.
AS_[is;is not]
the direct sum of U, V, and W.
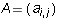 is said to be symmetric if
is said to be symmetric if
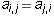 for all indices i and j. The same matrix is
said to be antisymmetric if
for all indices i and j. The same matrix is
said to be antisymmetric if 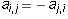 for all indices
i and j. Indicate which of the following are true; be sure that you
can either prove the assertion or give a counter-example.
AH_[2]
for all indices
i and j. Indicate which of the following are true; be sure that you
can either prove the assertion or give a counter-example.
AH_[2]
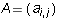 is anti-symmetric, then
is anti-symmetric, then 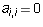 for all
indices i.
AS_[true;false]
for all
indices i.
AS_[true;false]
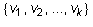 of U to a basis
of U to a basis 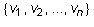 of V. Let W be the span of
of V. Let W be the span of 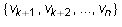 . Then V
is the direct sum of U and W
AS_[true;false]
Make sure you can either prove the assertion of give a counterexample.
SKIP_
p6
QM_[0;true;true]
Let U and W be arbitrary subspaces of a vector space V. Let
. Then V
is the direct sum of U and W
AS_[true;false]
Make sure you can either prove the assertion of give a counterexample.
SKIP_
p6
QM_[0;true;true]
Let U and W be arbitrary subspaces of a vector space V. Let 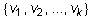 be a basis for the subspace
be a basis for the subspace 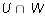 .
Extend this to a basis
.
Extend this to a basis 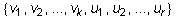 of U.
Extend the basis again to a basis
of U.
Extend the basis again to a basis 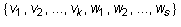 of W.
AH_[2]
of W.
AH_[2]
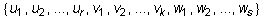 is a basis for U + W.
AS_[true;false]
is a basis for U + W.
AS_[true;false]
 V).
AS_[true;false]
V).
AS_[true;false]
 are said to be perpendicular to
each other if the dot product of any vector in U with any vector in V is
always zero. Is it true that, if U and W are perpendicular, then
U + W is the direct sum of U and W? Why?
AS_[yes;no]
SKIP_
p8
QM_[0;no;no]
Let U, V, and W be subspaces of vector space such that U + W = V + W.
AH_[2]
are said to be perpendicular to
each other if the dot product of any vector in U with any vector in V is
always zero. Is it true that, if U and W are perpendicular, then
U + W is the direct sum of U and W? Why?
AS_[yes;no]
SKIP_
p8
QM_[0;no;no]
Let U, V, and W be subspaces of vector space such that U + W = V + W.
AH_[2]