H_
Homomorphisms
SKIP_
p1
QM_[0;linear map;linear map;not a linear map;linear map;not a linear map;not a linear map]
Which of the following spaces are necessarily linear maps?
AH_[2]
-
AS_[linear map;not a linear map]
h((x, y, z)) = (2x+y, 2z+x-y)
-
AS_[linear map;not a linear map]
The map D from the rational functions of one variable into the rational
functions of one variable where D(f) = f', i.e. D(f) is the derivative of f.
-
AS_[linear map;not a linear map]
G((x,y)) = (0, 1)
-
AS_[linear map;not a linear map]
The map from the polynomials to the polynomials defined by
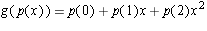 .
.
-
AS_[linear map;not a linear map]
The map from the polynomials to the polynomial defined by g(p(x)) = p(x+1)p(x-1)
-
AS_[linear map;not a linear map]
The determinant map det(a,b,c,d) = ad - bc.
SKIP_
p2
QM_[0;true;false;true;false]
Let P be the vector space of polynomials of one variable with real coefficients.
AH_[2]
Which are the following are true? Be sure that you can either prove the
assertion or give a counterexample.
-
AS_[true;false]
The map D which maps every polynomial to its derivative is a linear map.
-
AS_[true;false]
The map D has an inverse.
-
AS_[true;false]
There is a linear map R from P to P such that D(R(p(x)) = p(x) for every
polynomial p(x) in P. (If it exists, what is it?)
-
AS_[true;false]
There is a linear map L from P to P such that L(D(p(x)) = p(x) for every
polynomial p(x) in P. (If it exists, what is it?)
SKIP_
p3
QM_[0;true;true;true;true;false]
Consider the vector space 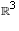 .
Be sure that you can either prove the
assertion or give a counterexample:
AH_[2]
.
Be sure that you can either prove the
assertion or give a counterexample:
AH_[2]
-
AS_[true;false]
The perpendicular projection of the vector (a, b, c) into the xy-plane is
a linear map. (The map is p((a, b, c)) = (a, b).)
-
AS_[true;false]
Let
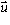 be any vector of unit length. The map f which maps
be any vector of unit length. The map f which maps 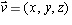 to the
vector
to the
vector 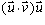 (where the dot indicates dot product)
is a linear map. This is called the component of
(where the dot indicates dot product)
is a linear map. This is called the component of 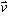 in the direction
in the direction 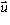 .
.
-
AS_[true;false]
Letting
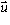 be as in the last part, the map p defined by
be as in the last part, the map p defined by 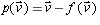 is a linear map. It is called the perpendicular projection into the
plane perpendicular to
is a linear map. It is called the perpendicular projection into the
plane perpendicular to 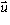 .
.
-
AS_[true;false]
The map p of the first part is the perpendicular projection into the plane
perpendicular to (0, 0, 1).
-
AS_[true;false]
The map p of the first part cannot be the perpendicular projection into the
plane perpendicular to any unit length vector other than (0, 0, 1).
SKIP_
p4
QM_[0;false;true;false;false;true;false;true]
Let f be a linear map from a vector space V to a vector space W.
Let S be a set of vectors in a vector space V, and f(S) be the
set 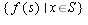 .
AH_[2]
Which of the following are true? Make sure you can either prove the
assertion or give a counter-example.
.
AH_[2]
Which of the following are true? Make sure you can either prove the
assertion or give a counter-example.
-
AS_[true;false]
If S is linearly independent, then so is f(S).
-
AS_[true;false]
If f(S) is linearly independent, then so is S.
-
AS_[true;false]
If S spans V, then f(S) spans W.
-
AS_[true;false]
If f(S) spans W, then S spans V
-
AS_[true;false]
If S spans V, then f(S) spans the rangespace of f.
-
AS_[true;false]
If S is a basis of V, then f(S) is a basis of W.
-
AS_[true;false]
If f is non-singular (i.e. one-to-one), and f(S) spans W, then S spans V.
SKIP_
p5
QM_[0;true;false;true;false;6;0]
Consider the function f from the polynomials of degree at most 5 to
the polynomials of at most 7 defined by 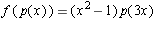 Answer the following are necessarily true. Make sure you
can either prove the assertion or give a counter-example.
AH_[2]
Answer the following are necessarily true. Make sure you
can either prove the assertion or give a counter-example.
AH_[2]
-
AS_[true;false]
The function f is a linear map.
-
AS_[true;false]
The rangespace of f is the set of all polynomials of degree at most 7
with roots at 1.
-
AS_[true;false]
The map f is non-singular.
-
AS_[true;false]
The map f is onto.
-
The rank of f is
AS_[0;1;2;3;4;5;6;7]
-
The nullity of f is
AS_[0;1;2;3;4;5;6;7]
SKIP_
p6
QM_[0;true;false;4;true;2]
Let f be a linear map from a vector space of dimension 4 to a vector space
of dimension 7. Answer the following questions; as usual, you should be
able to prove the assertion or give a counter-example.
AH_[2]
-
AS_[true;false]
The function f cannot be onto.
-
AS_[true;false]
The function f cannot be one-to-one.
-
If the nullity is zero, then the rank must be
AS_[0;1;2;3;4;5;6;7]
-
AS_[true;false]
If the rank is 4, then the nullity is zero.
-
If the rank is 2, then the nullity is
AS_[0;1;2;3;4;5;6;7]
.
SKIP_
p7
QM_[0;true;true;true;true;true]
Let f be a linear map from a vector space V to a vector space W.
Let S be a basis of the nullspace K of f. Let T be disjoint from S and
such that the union of S and T is a basis of V.
AH_[2]
-
AS_[true;false]
V is the sum of K and the span of T.
-
AS_[true;false]
V is the direct sum of K and the span of T.
-
AS_[true;false]
f(S) is the trivial subspace of the codomain of f.
-
AS_[true;false]
f(T) is a basis of the rangespace of f.
-
AS_[true;false]
The restriction of f to the span of T is an isomorphism
between the span of T and the rangespace of f.
SKIP_
p8
QM_[0.001;1;true;true;true;false]
Let V be a vector space and S be a basis of V.
AH_[2]
Make sure you can either prove the assertion or give a counterexample:
-
For every s in S, let
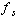 be the linear map from V to
be the linear map from V to 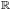 defined by
defined by 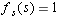 and
and 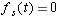 for all t in S other than s.
The rank of
for all t in S other than s.
The rank of 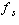 is
AC_[7]
.
is
AC_[7]
.
-
AS_[true;false]
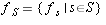 is linearly independent.
is linearly independent.
-
AS_[true;false]
There is a unique linear map g from V to
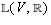 defined
by
defined
by 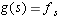 and this linear map is one-to-one.
and this linear map is one-to-one.
-
AS_[true;false]
If V is of finite dimension, then the linear map g is an isomorphism.
-
AS_[true;false]
The function g is always an isomorphism.
SKIP_
p9
QM_[0;true]
A linear map from a finite dimensional vector space to itself is one-to-one if and only
if it is onto.
AS_[true;false]
SKIP_
p10
QM_[0;10]
What is the dimension of the space of linear maps from a vector space of
dimension 5 to a vector space of dimension 2? Try to generalize from
problem 8. Can you generalize further?
AC_[7]
.
SKIP_
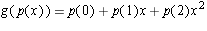 .
.
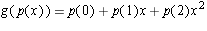 .
.
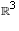 .
Be sure that you can either prove the
assertion or give a counterexample:
AH_[2]
.
Be sure that you can either prove the
assertion or give a counterexample:
AH_[2]
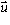 be any vector of unit length. The map f which maps
be any vector of unit length. The map f which maps 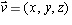 to the
vector
to the
vector 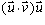 (where the dot indicates dot product)
is a linear map. This is called the component of
(where the dot indicates dot product)
is a linear map. This is called the component of 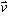 in the direction
in the direction 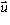 .
.
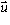 be as in the last part, the map p defined by
be as in the last part, the map p defined by 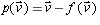 is a linear map. It is called the perpendicular projection into the
plane perpendicular to
is a linear map. It is called the perpendicular projection into the
plane perpendicular to 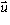 .
.
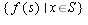 .
AH_[2]
Which of the following are true? Make sure you can either prove the
assertion or give a counter-example.
.
AH_[2]
Which of the following are true? Make sure you can either prove the
assertion or give a counter-example.
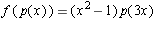 Answer the following are necessarily true. Make sure you
can either prove the assertion or give a counter-example.
AH_[2]
Answer the following are necessarily true. Make sure you
can either prove the assertion or give a counter-example.
AH_[2]
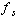 be the linear map from V to
be the linear map from V to 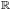 defined by
defined by 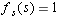 and
and 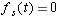 for all t in S other than s.
The rank of
for all t in S other than s.
The rank of 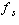 is
AC_[7]
.
is
AC_[7]
.
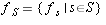 is linearly independent.
is linearly independent.
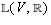 defined
by
defined
by 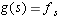 and this linear map is one-to-one.
and this linear map is one-to-one.