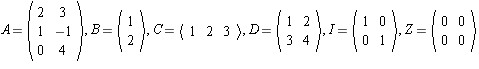
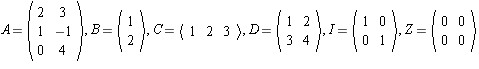
and
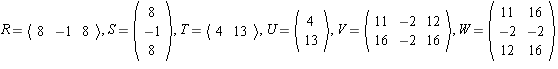
AH_[2]
 to itself defined by f(1) = 6.
AH_[2]
to itself defined by f(1) = 6.
AH_[2]
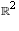 to
to 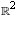 defined by
f((1,0)) = (3,-5) and f((0, 1)) = (1, 4). (As usual, I will often write
column vectors as row vectors -- you are expected to interpret them
correctly from the context.)
AH_[2]
defined by
f((1,0)) = (3,-5) and f((0, 1)) = (1, 4). (As usual, I will often write
column vectors as row vectors -- you are expected to interpret them
correctly from the context.)
AH_[2]
|
|
|
|
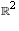 to
to 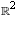 is defined
by the matrix
is defined
by the matrix 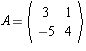 where the
matrix was defined with respect to the basis
where the
matrix was defined with respect to the basis 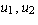 (in this order)
for the codomain and
(in this order)
for the codomain and 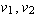 (in this order) for the domain.
Suppose the linear map g from
(in this order) for the domain.
Suppose the linear map g from  to
to 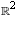 is defined
by the matrix
is defined
by the matrix 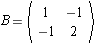 where the
matrix was defined with respect to the basis
where the
matrix was defined with respect to the basis 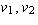 (in this order)
for the codomain and
(in this order)
for the codomain and 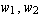 (in this order) for the domain. Let
h = f(g) be the composition of the two linear maps.
AH_[2]
(in this order) for the domain. Let
h = f(g) be the composition of the two linear maps.
AH_[2]
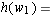 AC_[4]
AC_[4]
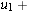 AC_[4]
AC_[4]
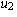 and
and 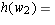 AC_[4]
AC_[4]
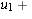 AC_[4]
AC_[4]
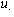 .
.
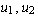 for the codomain
and
for the codomain
and 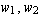 for the domain is:
for the domain is:
|
|
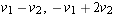 (in this order) is
(in this order) is
|
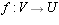 and
and 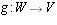 be linear maps of finite
dimensional vector spaces. Let
be linear maps of finite
dimensional vector spaces. Let 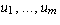 ,
, 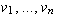 , and
, and
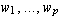 be bases of U, V, and W respectively. Let
be bases of U, V, and W respectively. Let 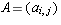 and
and 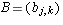 be
the matrices of f and g respectively, where each matrix is written using
the above bases (in the order specified). Let h = f(g).
AH_[2]
be
the matrices of f and g respectively, where each matrix is written using
the above bases (in the order specified). Let h = f(g).
AH_[2]
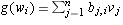 .
.
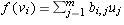 .
.
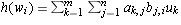 .
.
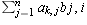 .
.
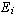 to a matrix is equivalent to
multiplying it on the left by the matrix
to a matrix is equivalent to
multiplying it on the left by the matrix 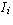 for i = 1, 2, ..., k.
Then the result of applying the operations
for i = 1, 2, ..., k.
Then the result of applying the operations 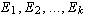 (in this
order) to the matrix is equivalent to multiplying the matrix on the left
by the product
(in this
order) to the matrix is equivalent to multiplying the matrix on the left
by the product 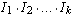 .
.
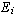 to a matrix is equivalent to
multiplying it on the left by the matrix
to a matrix is equivalent to
multiplying it on the left by the matrix 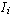 for i = 1, 2, ..., k.
Then the result of applying the operations
for i = 1, 2, ..., k.
Then the result of applying the operations 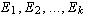 (in this
order) to the matrix is equivalent to multiplying the matrix on the left
by the product
(in this
order) to the matrix is equivalent to multiplying the matrix on the left
by the product 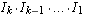 .
.
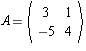 .
(Enter your answer as exact fractions, e.g. 4/3 rather than a decimal
approximation.)
AH_[2]
.
(Enter your answer as exact fractions, e.g. 4/3 rather than a decimal
approximation.)
AH_[2]
|
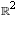 to itself defined by the
matrix
to itself defined by the
matrix 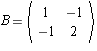 where we are
using the standard basis. Consider the basis
where we are
using the standard basis. Consider the basis 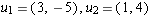 .
AH_[2]
.
AH_[2]
|
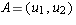 , then using the results of the
last exercise, one can calculate
, then using the results of the
last exercise, one can calculate 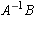 to be exactly
to be exactly
|
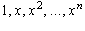 .
AH_[2]
.
AH_[2]